Wallpaper groups: 2. Theorems on Rotation and Translation

Theorem: characterization by two points

Two points P, Q and their image P', Q' uniquely defines a transformation.

Proof: Rotation has one fixed point, translation has none.
Suppose motion m1 and motion m2 both maps P to P' and Q to Q'.
Then the motion m1*m2^-1 has at least two fixed point P and Q, but no motion can have two fixed points, thus the assumption cannot be true.
End of proof.

Think about the action of translation or rotation on two points for a moment. It is obvious that two different transformations can not transform two points the same way.

Theorem: closure of rotation and translation

Suppose {t1, t2, …, tn} is a sequence of transformations, where each element is a rotation or translation.
The action of this sequence is equivalent to one of the following: A single rotation; a single translation; identity.

Proof: Pick any two distinct points P, Q, and let P', Q' be their image.
We know that distance[P,Q]==distance[P',Q'] because rotation and translation are distance preserving.
If P==P' or Q==Q', then we have a rotation around P or Q respectively.
If If P==P' and Q==Q', we have the identity.
Now suppose P≠P' and Q≠Q'.

If distance[P,P']==distance[Q,Q'], then it is a translation since translation moves every point to the same distance.

Finding the rotation center of given points P, Q, P', Q'.

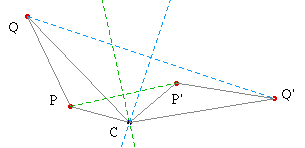
If distance[P,P']≠distance[Q,Q'], then it is a rotation.
Let C be the intersection of: (1) The bisector of PP' (2) the bisector of QQ'.
We show that C is the center of rotation taking P to P' and Q to Q'.
It suffice to show that the triangle PQC and P'Q'C are congruent.
Two triangles are congruent iff there is a pairing of equal length sides.
This is satisfied because we have distance[P,Q]==distance[P',Q'] (distance preserving transform), distance[P,C]==distance[P',C], and distance[Q,C]==distance[Q',C] (by construction).
End of proof.

In the above proof, we have assumed that multiple rotations and translations do not lead to transformations other than rotation or translation.
This can be proved by showing that rotation and translation are the only distance-preserving and sense-preserving transformations, and such property cannot be lost.

Theorem: product of two rotations

The product of two rotations centerd on A and B with angles α and β is equal to a rotation centered on C, where C is the intersection of:

(1) line AB rotated around A by -α/2.
(2) line AB rotated around B by β/2.

(if α+β==0, then its a translation. Proved above.)

Proof: Let's denote the rotation by A as r[A,α] and the rotation by B as r[B,β].
By the previous theorem, we know that the new rotation center C of 2 given rotations is Intersect[LineBisect[P,P'],LineBisect[Q,Q']], where P' is the image of a point P, and Q' is the image of Q (assuming P≠Q).
Now, let P := A, so that P' == r[B,β][A] since A rotated around itself is itself, and let Q be r[A,-α][B], so that Q' == B, since after the first rotation Q coincides with B, and rotating around itself doesn't change.
Now, the bisector of segment[P,P'] is just A rotated around B by β/2, due to our choice of P.
The bisector of segment[Q,Q'] is just B rotated around A by -α/2, due to our choice of Q.
End of proof.

This could also be proven easily with analytic geometry.

Theorem: parallel lines and angle of rotation

Under a rotation, the angle formed by any line m and its image m' is the angle of the rotation.

Proof: If a line n passes the center of rotation, then by definition angle[n,n'] is the angle of the rotation.
For any line m, there is a parallel line n that passes the center of rotation.
Rotation transform parallel lines to parallel lines.
We have m parallel to n and m' parallel to n'.
Since two sets of parallel lines intersects at the same angle, thus angle[n,n']==angle[m,m'].
End of proof.

Note: Two lines forms four distinct angles: α, π-α, -α, -(π-α).
You may workout the details how the theorem and proof applies

Theorem: rotation angle additivity

A rotation through angle α and another through angle β is equal to a single rotation with angle α+β.
If α+β==0 then it is a translation or identity.
It is a translation if centers of rotation are distinct, else identity.

Proof: This theorem follows from the theorem of Parallel Lines and Angle of Rotation, the rotation angle is the intesection of a line and its image.
Pick a line m.
We have its image m', and its image m'' after two rotations.
m and m' intersect at A with angle α.
m' and m'' intersect at B with angle β.
We want to know the intersection of m and m''.
Translation of m'' from B to A preserves all the angles.
The angle of intersection of m and m'' is the sum of α and β.
End of Proof.

Exercise

Use analytic geometry to prove the rotation product theorem.
Find the product r[{a1,a2},α]*t[{v1,v2}] in terms of their parameters. Likewise for t[{v1,v2}]*r[{a1,a2},α] and r[{a1,a2},α]*r[{b1,b2},β].
Suppose α+β≠0, then r[A,α]*r[B,β]==r[C,γ]. Consider the transformation t:R^2→R^2 defined as t[X]:= r[A,α]*r[X,β], where α and β are constants and A is a fixed point. What kind of transformation is t? (hint: rotation product theorem is the key)

Some Formulas

The product of a rotation followed by a translation:

r[{x, y}, α]*t[{a,b}] ==
r[{1/2*(a + 2*x - b*Cot[α/2]),
   1/2*(b + 2*y + a*Cot[α/2])}, α]

The product of a translation followed by a rotation:

t[{a,b}]*r[{x, y}, α] ==
r[{-(a/2) + x - 1/2*b*Cot[α/2],
   -(b/2) + y + 1/2*a*Cot[α/2]}, α]

The product of two rotations (α+β ≠ 0):

r[{a1, a2}, α]*r[{b1, b2}, β] ==
r[{1/2*Csc[(α + β)/2]*
    ((-a2 + b2)*Cos[(α - β)/2] +
      (a2 - b2)*Cos[(α + β)/2] +
      a1*Sin[(α - β)/2] -
      b1*Sin[(α - β)/2] +
      a1*Sin[(α + β)/2] +
      b1*Sin[(α + β)/2]),
   1/2*Csc[(α + β)/2]*
    ((a1 - b1)*Cos[(α - β)/2] +
      (-a1 + b1)*Cos[(α + β)/2] +
      a2*Sin[(α - β)/2] -
      b2*Sin[(α - β)/2] +
      a2*Sin[(α + β)/2] +
      b2*Sin[(α + β)/2])},
  α + β]