The 17 Wallpaper Groups
For reference purposes, here are some tables and illustrations of the 17 wallpaper groups.
Wallpaper Group Notations
Various notations have been invented for the 17 wallpaper groups. The most widely used is the crystallographic notation adopted by the International Union of Crystallography. A recent and more mathematically sound system is devised by J. H. Conway, called the orbifold notation. (The idea is due to William Thurston)
The Orbifold Notation
{o, 2222, **, xx, *2222, 22*, 22x, x*, 2*22, 442, *442, 4*2, 333, *333, 3*3, 632, *632}
To completely understand orbifold and orbifold notation, a background in topology is required. For those who are ignorant of topology (including the author), the following is a helpful description: One can think that orbifold notation as consisting of symbols that represent the generators of the group. A integer n indicate the presence of n-fold rotations. A asterisk “*” indicate presence of reflections. A cross “x” indicates presence of glide reflections. For example, the group 442 consists of two distinct sets of 4-fold rotations and a set of 2-fold rotations. If the numbers come after the asterisk, then it means those rotation centers are the intersection of mirror lines. For example, the group *442 has all rotations centered on mirror lines. The group 4*2 has only the 2-fold rotation on mirror lines. Conway emphasize that to think of orbifold notation as generators is really missing the point. The revolutionary feature of orbifold notation is that it uses topology to explain symmetry, and results a more geometric understanding than groups. (those interested in orbifold should see J. H. Conway's paper and related websites, the scanned article is available at the Reference Section)
Here's a excerpt from Conway's paper for those mathematically advanced readers.
In this paper a surface group will be a discrete group of isometries of one of the following three surfaces:
- the sphere
- the Euclidean plane
- the hyperbolic plane.
These are all the simply-connected surfaces of constant Gaussian curvature.
We shall present a simple and uniform notation that describes all three types of group. Since this notation is based on the concept of orbifold introduced by Bill Thurston, we shall call it the orbifold notation.
Roughly speaking, a orbifold is the quotient of a manifold by a discrete group acting on it. It therefore has one point for each orbit of the group on the manifold (Orbifold = Orbit-manifold).
(See also: Wikipedia on Conway's orbifold notation)
The Crystallographic Notation
{p1, p2, pm|p1m, pg|p1g, pmm|p2mm, pmg|p2mg, pgg|p2gg, cm|c1m, cmm|c2mm, p4, p4m|p4mm, p4g|p4gm, p3, p3ml, p3lm, p6, p6m|p6mm}
Excerpt from Doris Schattschneider's paper (The Plane Symmetry Groups: Their recognition and notation. American Math Monthly. vol 85, pp. 439-450.)
The crystallographic notation consists of four symbols which identify the conventionally chosen “cell,” the highest order of rotation, and other fundamental symmetries. Usually a “primitive cell” (a lattice unit) is chosen with centers of highest order of rotation at the vertices. In two cases a “centered cell” is chosen so that reflection axes will be normal to one or both sides of the cell. The “x-axis” of the cell is the left edge of the cell (the vector directed downward). The interpretation of the full international symbol (read left to right) is as follows: (1) letter p or c denotes primitive or centered cell; (2) integer n denotes highest order of rotation; (3) symbol denotes a symmetry axis normal to the x-axis: m (mirror) indicates a reflection axis, g indicates no reflection, but a glide-reflection axis, l indicates no symmetry axis; (4) symbol denotes a symmetry axis at angle α to x-axis, with α dependent on n, the highest order of rotation: α == 180 degree for n==1 or 2, α == 45 degree for n == 4, α == 60 degree for n == 3 or 6; the symbol m, g, l are interpreted as in (3). No symbos in the third and fourth position indicate that the group contains no reflections or glide-reflections…
[The four alphanumeric symbols can be shortened without loss of identification and the shortened form is most popular.]
Many information about the group is indicated explicitly by the orbifold notation, including:
- The presence or absence of rotations (indicated by integers, with highest order being the max integer).
- The presence or absence of reflection (indicated by *).
- The presence or absence of glide reflection (indicated by x).
| ID | Orbifold notation |
IUC notation |
Possible Lattice types |
quotient space | degree |
|---|---|---|---|---|---|
| 1 | o | p1 | ▰ ,▮ ,♦ ,■,▲ | torus | 2 |
| 2 | 2222 | p2 (p2ll) | ▰,▮,♦,■,▲ | closed pillowcase | 2 |
| 3 | ** | pm (p1ml) | ▮,■ | cylinder | 1 |
| 4 | xx | pg (p1gl) | ▮,■ | Klein bottle | 1 |
| 5 | *2222 | pmm (p2mm) | ▮,■ | square | 1 |
| 6 | 22* | pmg (p2mg) | ▮,■ | open pillowcase | 1 |
| 7 | 22x | pgg (p2gg) | ▮,■ | nonorientable football | 1 |
| 8 | x* | cm (c1ml) | ♦,■,▲ | Möbius strip | 1 |
| 9 | 2*22 | cmm (c2mm) | ♦,■,▲ | 4,4,2 turnover, slit along 4,4 | 1 |
| 10 | 442 | p4 | ■ | 4,4,2 turnover | 0 |
| 11 | *442 | p4m (p4mm) | ■ | 4,4,2 triangle | 0 |
| 12 | 4*2 | p4g (p4gm) | ■ | 4,4,2 turnover, slit along 4,2 | 0 |
| 13 | 333 | p3 | ▲ | 3,3,3 turnover | 0 |
| 14 | *333 | p3ml | ▲ | 3,3,3 triangle | 0 |
| 15 | 3*3 | p3lm | ▲ | 6,3,2 turnover, slit along 3,2 | 0 |
| 16 | 632 | p6 | ▲ | 6,3,2 turnover | 0 |
| 17 | *632 | p6m (p6mm) | ▲ | 6,3,2 triangle | 0 |
Visual Representation of Wallpaper Groups
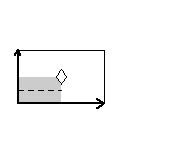
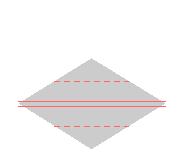
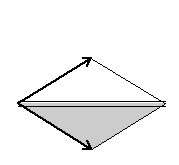
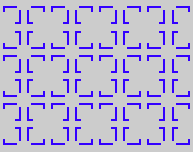
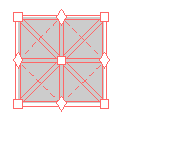
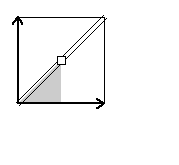
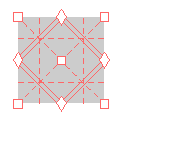
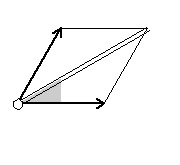
Here are visual representations of the 17 wallpaper groups. The first column contain representative wallpapers for each group. The wallpaper design is obtained by applying all symmetry elements to a L shaped motif. The symmetry elements themselves are indicated in pink colored symbols, superimposed on the wallpaper design. (Arrows indicating translations are not shown since they can be easily infered from the distance between the L motifs.) The second column is the wallpaper itself without the symmetry indicators. The top of third column is the group's symmetry elements in a unit cell. The bottom is its generators. The boundary is a unit cell. The gray area is its fundamental region. The generators are chosen as to always include two non-parallel translations. Such a set are suited for adoption by computer graphics algorithms.
| 2-fold center of rotation | |
| 3 | |
| 4 | |
| 6 | |
| axis of reflection | |
| axis of glide reflection |
| Wallpaper and its symmetries | Wallpaper | Symmetries and generators |
|---|---|---|
 |
 {1,o,p1} {1,o,p1} |

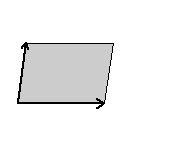 |
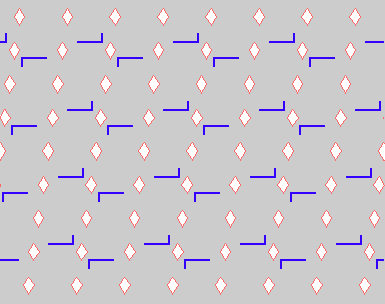 |
 {2,2222,p2} {2,2222,p2} |

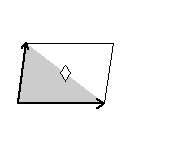 |
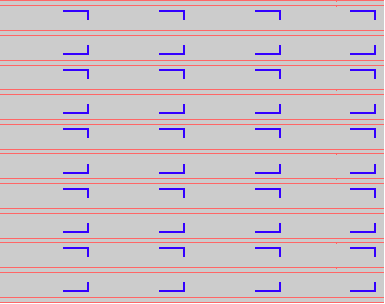 |
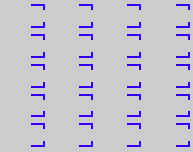 {3,**,pm} {3,**,pm} |

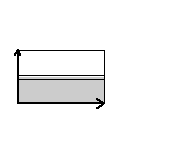 |
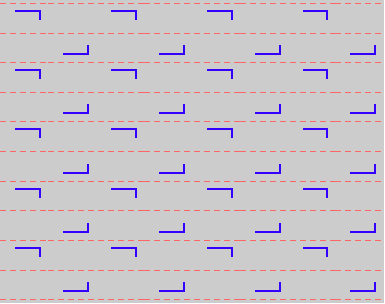 |
 {4,xx,pg} {4,xx,pg} |
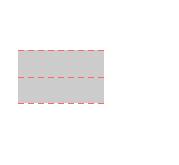
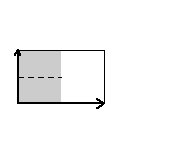 |
 |
 {5,*2222,pmm} {5,*2222,pmm} |
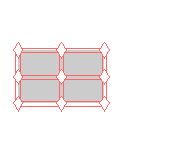
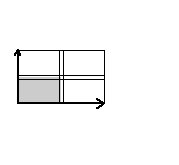 |
 |
 {6,22*,pmg} {6,22*,pmg} |

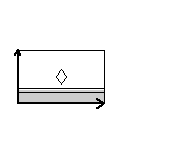 |
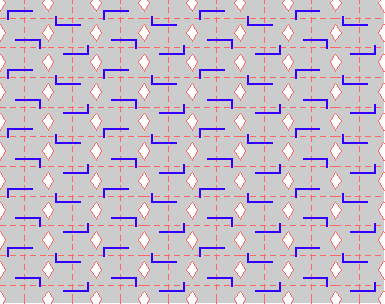 |
 {7,22x,pgg} {7,22x,pgg} |
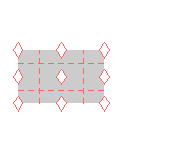
 |
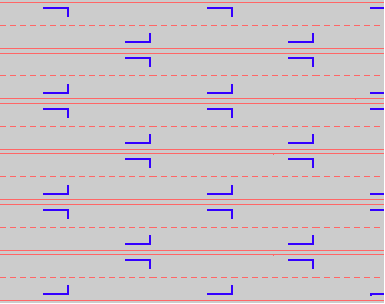 |
 {8,x*,cm} {8,x*,cm} |
 |
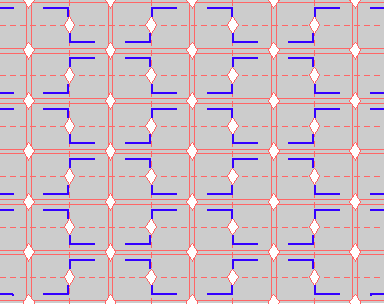 |
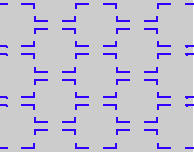 {9,2*22,cmm} {9,2*22,cmm} |
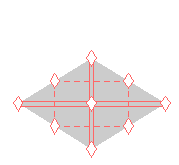
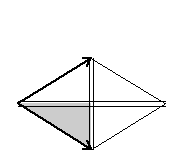 |
 |
 {10,442,p4} {10,442,p4} |
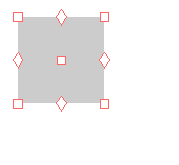
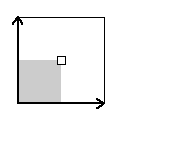 |
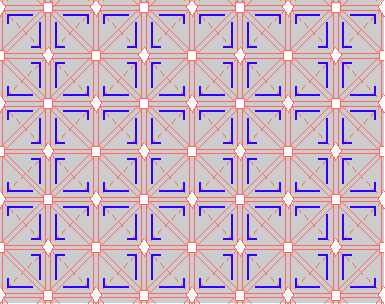 |
 {11,*442,p4m} {11,*442,p4m} |
 |
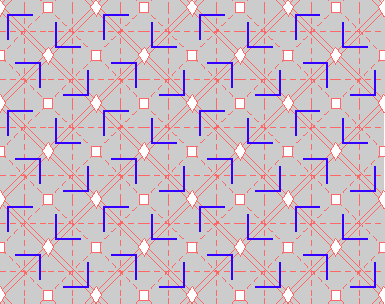 |
 {12,4*2,p4g} {12,4*2,p4g} |
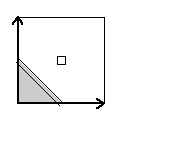 |
 |
 {13,333,p3} {13,333,p3} |

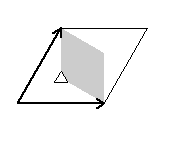 |
 |
 {14,*333,p3ml} {14,*333,p3ml} |
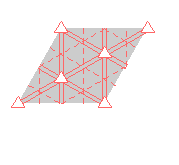
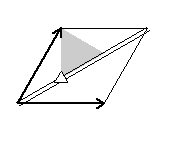 |
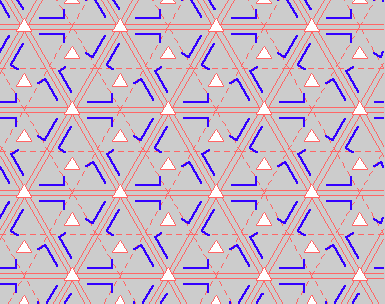 |
 {15,3*3,p3lm} {15,3*3,p3lm} |
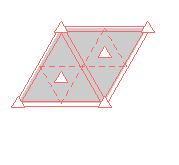
 |
 |
 {16,632,p6} {16,632,p6} |

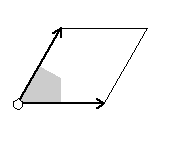 |
 |
 {17,*632,p6m} {17,*632,p6m} |
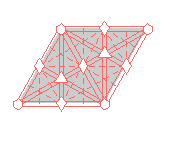
 |