Derivation and Classification of Groups
We devide the investigation into several categories. The group:
- Does not cotain translations
- Does not contain rotations.
- Contains at least one rotation.
- Contains translations
- All translations are parallel.
- Does not contain rotations.
- Contains at least one rotation.
- Not all translations are parallel
- Does not contain rotations.
- Contains at least one rotation
- The least positive rotation angle is 2*π/2.
- The least positive rotation angle is 2*π/3.
- The least positive rotation angle is 2*π/4.
- The least positive rotation angle is 2*π/6.
- The least positive rotation angle is not one of 2*π/n, where n is 2, 3, 4, or 6.
- All translations are parallel.
Group category 1.1
Does not contain translations or rotations.
There can be only the trivial group in this category, whoes only member is the identity.
Group category 1.2
Contains rotations only.
For all groups in this category, all rotations must have the same center. This is so because of the theorem Distinct Rotations Guarantees a Translation. Here's another proof. suppose p and q are two rotations in this group with different centers. By the additivity of angles of rotation theorem, p^-1*q*p*q^-1 has angle 0, thus it must be a translation or identity. It cannot be a translation since this category has none. It cannot be the identity since there is no fixed point. Thus our assumption that p and q are rotations with different centers cannot be true. (If p^-1*q*p*q^-1==I, then q*p==p*q, which cannot be true if p and q has distinct centers.)
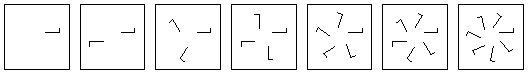
We have the cyclic group {r[P, (2*π/n)*m]}, where m is a variable integer 0 ≤ m < n, and n is a fixed integer 0 < n. (n cannot be real otherwise we wouldn't have a discontinuous group) The groups in this category include all cyclic groups of finite order.
Group category 2.1.1
Contains translations that's all parallel and there are no rotations.
Assume t[V] is one translation with the least length. Since t[V]^n==t[V*n], we have the group {t[V*n]} where n is a integer. There can be no element with length between t[V*n] and t[V*(n+1)] for any n because if t[U] is such element, then the element t[U]*t[V*n]^-1==t[U-V*n] has length smaller than t[V], contradicting that t[V] is chosen to have the shortest length. In this category, the only group we have is the cyclic group {t[V*n]} of infinity order.

Group category 2.1.2
Contains translations that's all parallel and there are rotations.
Any rotation in this category must have angle 2*π/2. This is so because by the theorem Transitivity of Translation, the presence of any translation will entail a translation that makes a angle α with the original, where α is any rotation angle present in the group. Since in this category all translations are parallel, α can only be 2*π/2.
The group {t[{n,0}]} of category 2.1.1 is a subgroup here. A lattice {t[{n,0}]} and a half-turn rotation constitutes a lattice of half-turns and half-turns on all midpoints of the lattice, by theorem 2-Fold Rotations on Midpoints of Lattice .
We have the group {t[{n,0}], r[{m/2,0},π]} where n and m are variable integers. This is the only group in this category. Suppose there is another rotation r[{d1,d2},2*π/2]. Now the product of two distinct half-turns is a translation with twice the distance between the half-turn centers. (think of the action on the rotation centers) If {d1,d2} is not on the lattice line t[{n,0}], then the new translation is not parallel to it, thus not allowed here. If {d1,d2} is on the lattice line but not one of {m/2,0}, then r[{d1,d2},π]*r1 where r1 is the closest rotation will give us a translation with length smaller than {1,0}, contradicting that t[{1,0}] has the shortest length.
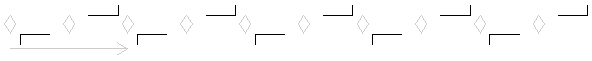
The only group in this category is {t[{n,0}], r[{m/2,0},π]}.
Group category 2.2.1
Contains non-parallel translations but no rotations.
Two non-parallel translations gives a lattice of translations. Suppose t[U] and t[V] are the standard basis vectors. There can be no other translation other than t[U*m+V*n]. If there is, then it must fall inside or on the side of a parallelogram formed by the lattice. The distance from it to any of the coners must be less then the length of the side, therefore contradicting that the basis vectors are chosen to have the shortest lengths.

The only group in this category is the plane lattice of translations {t[U*m+V*n]}.
Group category 2.2.2.1
Contains non-parallel translations and rotations where the least positive angle is 2*π/2.
π is the only possible angle here because any other would imply a angle less than 2*π/2. By theorem 2-Fold Rotations on Midpoints of Lattice, we have a lattice of half-turns with half the scale of the translation lattice. There can be no other rotations. Proof outline:
- The rotation lattice forms a array of parallelograms with sizes half of that translation lattice.
- The distance between a point on or inside a parallelogram to its nearest corners is less than the length of a shortest side. Twice of that distance is less than twice of the shortest side.
- Suppose there is a half-turn at P. P falls on or inside one of the parallelograms. The result of two half-turns equals a translation twice as long as the distance between half-turn centers.
- The half-turn at P followed by a nearest half-turn is a translation with length less than twice of the shortest side, which means it is less than the shortest side of the translation lattice. This is impossible since we've chosen the least length translations for the translation lattice. Thus there cannot be half-turns other than those on the half-turn lattice.
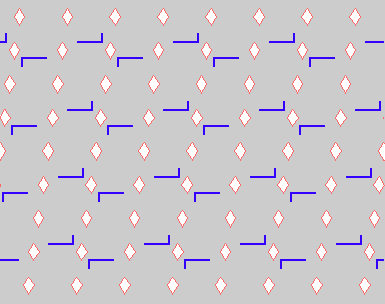
The only group in this category consists of a plane lattice of translations and a lattice of half-turn with half the scale: {t[U*m+V*n],r[(U*m+V*n)/2,2*π/2]}.
Group category 2.2.2.2
Contains non-parallel translations and rotations where the least positive angle is 2*π/3.
All rotations must have angle a integer multiple of 2*π/3, because any other would imply a angle less than 2*π/3. Suppose a rotation has angle 2*π/2. By theorem of addictivity of rotation angles, and by combining rotations, we'd get a angle less than 2*π/3 -- not allowed in this category.
We have t1:=t[P] and r1:=r[{0,0},2*π/3] with P:={1,0}. By transitivity of translation, we have t2:=t[Q]==r1^-1*t1*r1, where Q:=r1[P]. P and Q are vectors forming a angle 2*π/3, thus the subgroup {t[P*m+Q*n]} forms a triangular lattice. By transitivity of rotation, we have a lattice of rotations {r[P*m+Q*n,+-2 π/3]} as well. Now r2:=r1*t1 is a new rotation on a center of the triangle lattice, and by theorem transitivity of rotation, we have another lattice of rotations. Similarly, r3:=t1*r2 is new lattice of rotation. Thus, r1, r2, and r3 forms three "interlocking" triangle lattices.
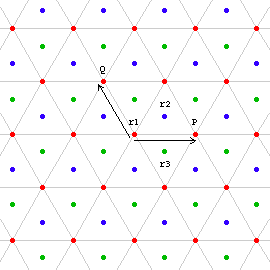

These are all the elements in this group, and there cannot be others. The proof is similar to the one discussed previously: if E is a rotation (with positive angle) that is not on one of the triangle lattice, and F is a rotation (with positive angle) on the lattice nearest to E, then E*F^-1 is a translation with length shorter than 1, contradiction our assumption.
Group category 2.2.2.3
Contains non-parallel translations and rotations where the least positive angle is 2*π/4.
Here we have possible angles 2*π/4*m, where m is a integer. This includes 2*π/2 angles. There are no other angles because that would imply 2*π/4 is not the smallest.
We have t1:=t[P] and r1:=r[{0,0},2*π/4] with P:={1,0}. By transitivity of translation, we have t2:=t[Q]==r1^-1*t1*r1, where Q:=r1[P]. P and Q are vectors forming a angle 2*π/4, thus the subgroup {t[P*m+Q*n]} forms a square lattice. By transitivity of rotation, we have a lattice of rotations as well (i.e. {r[P*m+Q*n,2*π/4*l]}).
Each rotation center is also a 2-fold rotation center. By theorem 2-Fold Rotations on Midpoints of Lattice, all midpoints between coners of our square lattice are 2-fold centers including the midpoint of all squares. We now show that the midpoint of all squares are actually 4-fold rotation centers. The product r1*t1 is a rotation r[{1/2,1/2},2*π/4] that is on the center of a square. By transitivity of translation, all centers of squares are 4-fold rotation centers.
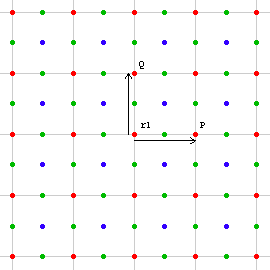
In this category, we have 2 classes of 4-fold rotation centers, and 1 class of 2-fold rotations, and translations. There are no others. The proof is similar to the above.
Group category 2.2.2.4
Contains non-parallel translations and rotations where the least positive angle is 2*π/6.
In this category, 2 and 3-fold rotation are also possible because 2*π/3==2*(2*π/6) and 2*π/2==3*(2*π/6). 4-fold rotation is not possible because by theorem rotation angle additivity, adding the angles of two possible rotations 2*π/4 + 2*π/6 == 2*π*5/12 results a angle not possible as a wallpaper group by theorem Crystallographic Restriction.
As before, we have t1:=t[P] and r1:=r[{0,0},2*π/6] with P:={1,0}. By transitivity of translation, we have t2:=t[Q]==r1^-1*t1*r1, where Q:=r1[P]. P and Q are vectors forming a angle 2*π/6, thus the subgroup {t[P*m+Q*n]} forms a triangle lattice. By transitivity of rotation, we have a lattice of rotations as well (i.e. {r[P*m+Q*n,2*π/6*l]}). Each of 6-fold rotation center is also a 3-fold rotation center, thus the discussion in group category 2.2.2.2 also applies here. Thus, we have a triangle lattice of 6-fold rotations, and every center of triangle is a 3-fold rotation. Since every 6-fold rotation center is also a 2-fold rotation center, and by theorem 2-Fold Rotations on Midpoints of Lattice, all midpoints of our lattice contains a 2-fold rotation. Thus far we have the group {t[P*m+Q*n],r[P*m+Q*n,2*π/6*l],r[R*m+S*n,2*π/3*l],r[(P*m+Q*n)/2,2*π/2*l]} with P and Q forming a angle 2*π/6 and are equal in length, R and S are vectors such that R:=r[2*π/12][P]*Sqrt[3]/3*Length[P], S:=r[2*π/12][Q]*Sqrt[3]/3*Length[Q]. (The elements r[R*m+S*,2*π/3*l] are the 3-fold rotations on the triangle lattice and centers of triangles.)
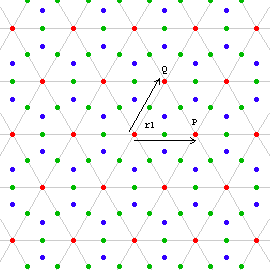

There are no other 2-fold or 3-fold rotation centers as discussed in the theorem 2-Fold Rotations on Midpoints of Lattice, and group category 2.2.2.2. There cannot be other 6-fold rotations either, because, similar to previous discussions, any other 6-fold rotaton not on the lattice combined with a nearest 6-fold rotation on the lattice in reverse direction will result a translation with length less than 1, contradicting our assumption that that the shortest length of translation is 1.
Group category 2.2.2.5
Contains non-parallel translations and rotations where the least positive angle is not one of 2*π/n with n := {2,3,4,6}.
As by the theorem Crystallographic Restriction, there can be no group in this category.