On Meta Syntax, Formal Language, and Logic

(xah's rumination extempore, is when i have something on my mind and type as fast as i can to express it, where i dunno what am saying or where am i going, and you rip my brain out)

currently worrying about issues in meta syntax, such as BNF.

for example, there's these pages

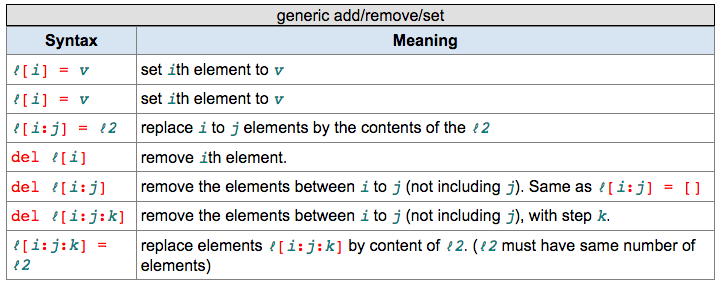
i'll be using CSS syntax here to discuss the issue, but the issue is about meta syntax language and applies to all.

you see those italized words? those represent variables. (for clarity, i'll angle bracke them in this post, like this ‹x›)

in CSS, this ‹tag› will match anything, where ‹tag› is any html element name. Since any html tags is a finite set, so, ‹tag› actually stands for a restricted set of strings, not ANY.

however, CSS selector is not just for html, but for xml as well. Meaning, the ‹tag› is potentially infinite, however, still not arbitrary string.

So, here we have a issue of what ‹x› actually means. It can be any element of a finite set, or it can be potentially infinite, or it sometimes can be arbitrary string.

by the way, the context of this articles, is about meta syntax, formal language, logic, and computer software documentation format. Basically, i write a lot tutorials, so i need to use some syntax to represent syntax.

I'm into formal languages, so i want my syntax to be precise as some variation of computable BNF or particular pattern matching language (say in Mathematica), but i also need it to be human readable, because it is used in tutorials. First question is whether it's possible the have a syntax description language that is very human readable (as suitable to be used in API or tutorial), i believe yes.

see also Pattern Matching vs Grammar Specification

the other thing is the naming of a variable ‹x›. For example, 「convertToFloat(‹integer›)」. There, the name “integer” gives reader a good sense of what string ‹integer› can be. One must be careful here, because by definition, ‹x› can stand for anything, a particular set of things, and the set can be infinite set, such as integers. The problem here is that, unless you actually define, by a formula, the precise meaning of ALL your ‹x›, otherwise a wrong naming introduces paradox or may be misleading.

for example, normally we'll see any of these in programing docs

「convertToFloat(‹integer›)」
「convertToFloat(‹i›)」
「add(‹n›)」
「convertToFloat(‹number›)」
「coordinate(‹x›, ‹y›)」

intuitively and sloppily, we understand what they mean without problems. (actually, with problems, but am not sure how extensive it is. See OOP Dot Notation, Dot Before Data or After? ) but they are not precise. For example, in any language, the format of a number is a specific pattern of sequence of symbols. Depending on whether it's python, java, lisp, html, you may have

e.g.
1234
o724
#724
x724
u\724

another example 「‹s›.replace(/‹regex›/,‹replace›)」 here, if you write 「‹x›.replace(/‹n›/,‹i›)」 it's still technically good, but misleading, because the “n” in ‹n› usually is taken to be a integer.

the important thing to note here is that, the NAMING of your pattern actually have significant significance. Something we don't think about much, but has great consequences.

In another way to look at this is that, if you think of your syntax as formal language, then the naming really doesn't matter (actually…), provided that you do have the complete system definition of all your ‹x› (which are basically patterns. a pattern language)

so, here we must consider, what you gonna do? When you write

「convertToFloat(‹integer›)」 or 「‹s›.replace(/‹regex›/,‹replace›)」 in a tutorial or lang documentation, do you actually go all the way and define all those ‹integer› and ‹s› etc? Is this practical such that it can be done in a tutorial?

meanwhile, you can take a sloppy and broader approach, such that anything ‹x› is just meant to be arbitrary symbol or sequence of symbols, and the naming (the english interpretation of the x in ‹x› is just a hint). But if this approach is taken, the naming actually has a meaning, and becomes critical, because 「convertToFloat(‹function›)」 would be dead wrong.

here's another example, from css, where you can't random name 「‹tag›[‹attr›="‹val›"]」 vs 「‹t›[‹a›="‹v›"]」

in the latter, since it's single letters, so it gives you a lot flexibility. But it's not intuitive. if you change their order 「‹a›[‹v›="‹t›"]」 it can still work, or even 「‹x›[‹y›="‹z›"]」 is good.

While using names {tag, attr, val} is intuitive. But here, note that each named placeholder has meaning attached to them.

here's another thing to consider. Sometimes we want to document function, we write

plusOne(‹args›)
plusOne(‹number›)

you see 2 very different approach? the question on my mind, is to logically clarify the whole ontology of this. Here, we are entering another level of semantics. Note, when you say “arg”, it means argument. Good. Note, when you say “number”, it means a number, also Good. Now consider this:

f(‹arg1›, ‹arg2›, …)
f(‹num1›, ‹num2›, …)

which one should you use? what's their differences? what is their consequence, to the following english wording for the function?

ok, the above is mostly about the naming of a pattern.

ok, but there are other issues. Sometimes, you want to write, for example in css:

「t1>t2」

「‹x›+‹y›=4」

here, we may have both ‹x› and ‹y› to be 2.

CSS example:

「‹t1›>‹t2›」

here, both ‹t1› and ‹t2› can be the same tag, say “div”.

but, sometimes we need to have a syntax that contains 2 different things. e.g. in math, typically it's done as a added condition in english, example

「‹x›+‹y›=4」 and x≠y.

that's simply ugly and out of it. (totally out of the realm of formal languages. (you know? it's interesting. In math, some subject say geometry or algebra, there are ofter different axioms or foundations. When you use a different foundation, all things, concepts, defintions, needs to be changed or rephrased. (am thinking universal algebra vs classic abstract algebra)))

anyway, i think i stop here. I started to write this because i was just working on this page

CSS Selector Syntax

recently i removed all the ‹› and 「」 brackets, because for most readers, it's distracting. The convention is to use italic for ‹x› instead. But that has lots of problems i recently discussed. Basically, using slated font is a rendering issue, it helps reading, but took out the formal language aspect.

also note, of all computer language documentation out there, none are specific and precise. All are rather extreme garbage. (fk the programer hackers scbgs and fk their moms) for a example of the garbage that another issue, see:

Optional Function Parameters in Computer Language Docs (the idiocy thereof)

see also related:

• JavaScript Context Dependent Semantics: p in o
• Python Syntax Soup: x in y

comment at https://plus.google.com/+XahLee/posts/7GDsk4L6Kiv