Category Theory Notes
Category theory formalizes mathematical structure and its concepts in terms of a labeled directed graph called a category, whose nodes are called objects, and whose labelled directed edges are called arrows (or morphisms).
A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object.
narrow definition of category
A category is:
- a collection of sets.
- a collection of bijection functions, that maps a set to another.
such that the following is true:
- (associativity) if f : a → b, g : b → c and h : c → d then h ∘ (g ∘ f) = (h ∘ g) ∘ f
- (identity) for every set, there is a identity function that maps the set to itself.
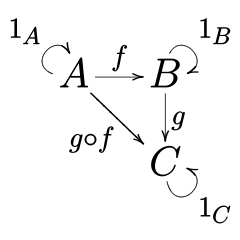
more generally, the sets are called “objects”, and the objects are usually some structure, such as groups.
and the function are called morphism (or arrows), and the function are often those that preserve some structure of the object. e.g. if the objects are groups, then the functions are homomorphisms.
Another example: if the objects are topological spaces, then the function are continuous functions.
so, for each class of objects, we use a particular class of functions. So, we have different categories, and usually we give each a name.
here's a table
| category name | object | morphisms |
|---|---|---|
| Mag | magmas | magma homomorphisms |
| Manp | smooth manifolds | p-times continuously differentiable maps |
| Met | metric spaces | short maps |
| R-Mod | R-modules, where R is a ring | R-module homomorphisms |
| Ring | rings | ring homomorphisms |
| Set | sets | functions |
| Grp | groups | group homomorphisms |
| Top | topological spaces | continuous functions |
| Uni | uniform spaces | uniformly continuous functions |
| VectK | vector spaces over the field K | K-linear maps |
a textbook: https://arxiv.org/abs/1803.05316
local mirror category_theory_brendan_fong_david_spivak_2018-03.pdf