What is the Nature of Eigenvector?
What is Eigenvalues and eigenvectors?
An eigenvector of a square matrix A is a non-zero vector v that, when the matrix is multiplied by v, yields a constant multiple of v, the multiplier being commonly denoted by λ. That is:
A v = λ vThe number λ is called the eigenvalue of A corresponding to v.
here's a funtional style of description.
eigenvector and eigenvalue are special elements associated with some linear function of vector space.
Let f:𝕍→𝕍 be a linear function on vector space 𝕍. A eigenvector of f is any none-zero element v in 𝕍 such that
f[v] == λ*v
for some constant λ. λ is called the eigenvalue for the eigenvector v.
here's a illustration of eigenvector.
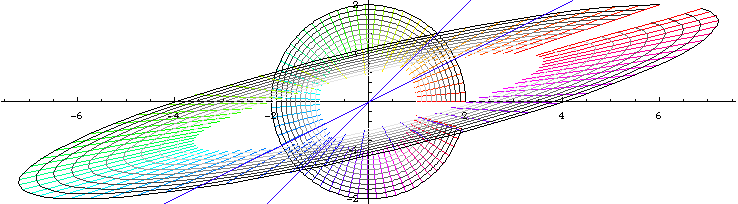
{{3,-2},{1,0}}. The matrix has two independent eigenvectors {1,1} and {2,1}, indicated by blue lines. Their significance is that points on those lines will remain on those lines.
eigenvector is also called characteristic vector because it characterize the linear function.
not all linear function has eigenvectors. For example, rotation around origin (on 2D vectors) is a linear function, but doesn't have eigenvector. See also: Nature of Linear Transformation .
- On the Naming of Eigenvector and the Igon Value Problem
- the Nature of Associative Property of Algebra
- The Geometric Significance of Complex Conjugate
- The Significance of Complex Numbers: Frobenius Theorem
- What is Riemann Surface? Understanding the Concept Without Math
- Geometry: Transformation of the Plane II