Math: Fibonaci Sequence Video Fallacy 📺

Beware of Math Fallacies Spreading on The Net

Recently this video is spreading fast on the net.

A beautiful video indeed, but filled with fallacies.

It would be good for math teachers to use this vid as a intro, then proceed to go into detail of every piece of math shown in the video, and point out the parts that are false.

First, there's the Fibonacci sequence: {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …}. This is formed by adding the previous 2 terms, starting with 0 and 1.

[0:32] The Fibonacci spiral, constructed by fitting quarter circle arcs on stacks of squares with sides of Fibonacci numbers. The spiral formed is a approximation of a spiral called the Equiangular Spiral (aka logarithmic spiral).

The Fibonacci spiral isn't a true spiral. That is, it has kinks at every place the square connects (to see the kinks, think of a circle. A circle is a curve that has constant curvature at any point on the curve. Different sized circle have different curvatures. So, by connecting arcs of 2 circles from different sizes, the curvature will suddenly jump at the connection point. Although, such connection will be superficially smooth, but on a second level it is not smooth (this is the idea of derivative). You cannot design roads, train tracks, or roller coasters by just connecting circles of different sizes.).

Here, you should remember that the stacking of circular arcs as done by Fibonacci spiral is only a approximation to a particular equiangular spiral, called Golden Spiral.

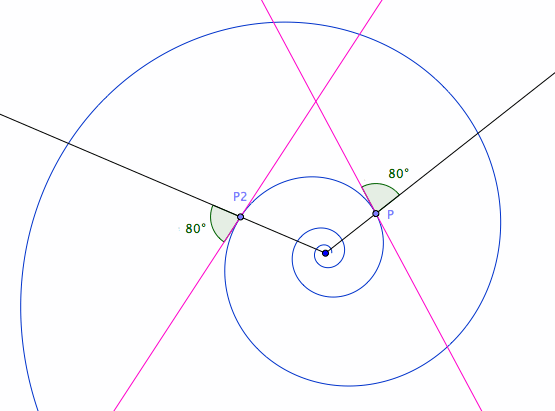
A easy way to understand equiangular spiral is that it's a spiral such that its growth rate is constant. (For much more and many pictures, see: Equiangular Spiral.)

The equiangular spiral is a family of spirals, with a constant angle as parameter. The Fibonacci spiral is a approximation of just one of them, called the Golden spiral .

then, they fit this spiral to the nautilus shell. Note again that it's the equiangular spiral the shell is based on, not the Fibonacci stacks of circular arcs, and nor is the shell shaped like the particular equiangular spiral that Fibonacci spiral is approximating.

Here is a quote from Wikipedia Nautilus:

The nautilus shell presents one of the finest natural examples of a logarithmic spiral, although it is not a golden spiral.

[1:30] then, they draw a rectangle outline of the shell, then cut it in half, then take a diagonal and sweep it down... as if to show that a rectangular hull of the shell has the right proportions to construct the golden rectangle. This is pure garbage.

[1:41] then, they sweep a circle and spit out speeds at every angle of (2*π - 2*π/φ) radians to show how it forms the sunflower pattern. This is also borderline of pseudoscience. You can spit out seeds in such a regular way but using just about any other constant angle and still be able to show the result being similar to the patterns of sunflower seed's arrangement.

[2:53] then, they pick out certain dots of the sunflower seeds, connect lines, to form the pattern on dragonfly's wings. This is again purely fairy tale. Am not quite sure what rule they used to pick out the dots. But it doesn't matter. The closest real math this part of vid is trying to show the idea of Voronoi diagram and Delaunay triangulation .

Here is how it works. Given a bunch of dots on a paper, suppose you need to draw lines as to form borders between all the dots (think of each dot as a person, and you want to create a fair personal space among all people). One way, is to have the border such that any point on the border is equal-distant between the 2 neighboring dots. Such a border is called the Voronoi diagram. So, some plant's cell patterns, insect wing patterns, might be based on this principle because the equal-distance property is optimal under the circumstances of physical or biological constraints. Also remember, you have to start with placement of dots first. If the dots are arranged regularly, then the Voronoi diagram would also be regular. For example, if the dots are arranged in a square grid, then the Voronoi diagram is just a square grid. If the dots are arranged in a triangular grid, then its Voronoi diagram is a honeycomb tiling.

Even if we suppose that the pattern of a dragonfly's wings is a Voronoi diagram (which, clearly it is not just by observing photos, except in some artificially limited regions), that still leaves the more essential question of how the dots are arranged.

In summary, it is possible to make a convincing animation that suggests false relations or proofs between any math number or curve. Mathematicians never relied on visual illustration as proofs, and the fallacy caused by visual illustrations has moved many mathematicians to completely avoid using figures at all in serious publications since about ~1700s or was it ~1800s.

The Fibonacci sequence is a rife source of math mysticism. There are lots of websites telling you how it connects to everything in nature, art, or god. The good news is, starting in about 2007, articles debunking the Fibonacci myth started to appear. For more and links, see: Math Mysticism: is Hurricane Shape a Fibonaci Spiral? .