Knitting, Chinese Knots, Braid Theory

By Xah Lee. Date: 2010-04-30. Last updated: 2019-03-22.

Am fascinated by the math aspects of knitting… e.g. the pure math aspect of how those threads are inter-woven, such as in Braid theory.

Knitting red courses reverse stockinette garter tvy5d — Knitting. [image source 2010-05-01 http://en.wikipedia.org/wiki/File:Knitting_red_courses_stockinette_garter.png ]

cable knit 7tvvx — cable knit [image source ~~https://www.etsy.com/listing/122355338/giant-cable-knit-blanket-or-throw~~]

cable knitting — Cable kniting. [image source 2010-05-01 http://en.wikipedia.org/wiki/File:Knitcable.jpg ]

Besides the math aspect of which thread are intertwined with which other threads in what way, it is also possible to create a pattern on the surface. What such patterns are possible, how are they made, must by itself be a complex theory.

Serweta-na drutach2 — Lace tablecloth made using knitting needles.

Chinese Knots

Also related is Chinese knotting.

chinese knot1 — Chinese knot. This one has the characteristics of fractal. [image source ~~http://www.ojuang.com/chineseknots.html~~]

9chinese-knot — Chinese knots. [image source http://www.chinahighlights.com/travelguide/culture/knot.htm]

chinese knot 7-luck — Chinese knot. [image source http://chineseknotting.org/luck/]

Chinese butterfly knot — Chinese knots. [image source 2010-05-01 http://en.wikipedia.org/wiki/File:Chinese_Butterfly_Knot.jpg ]

Discovered this fantastic book, free: Encyclopedia Of Needlework 1884, By Thérèse De Dillmont. At http://www.gutenberg.org/files/20776/20776-h/chapter_11.html

It provides in-depth coverage, with hundreds of clear illustrations, many of which shows the pure weaving beauty of math.

Basket Weaving

weaving trad1 — A weaving pattern (Wickerwork) commonly found in Asian chairs made of rattan.

Celtic Knots

Decorative Weaving Patterns

knots pattern disc — Left: From “Islamic Designs for artists and craftspeople”, by Eva Wilson, 1988. Above right, from a book.

weaving pattern star — Left: From “Islamic Designs for artists and craftspeople”, by Eva Wilson, 1988. Above right, from a book.

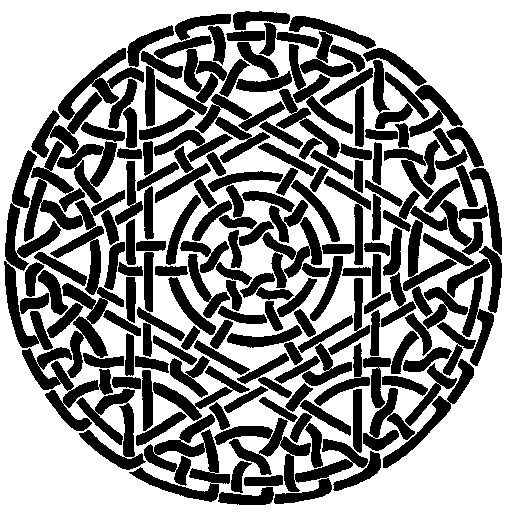
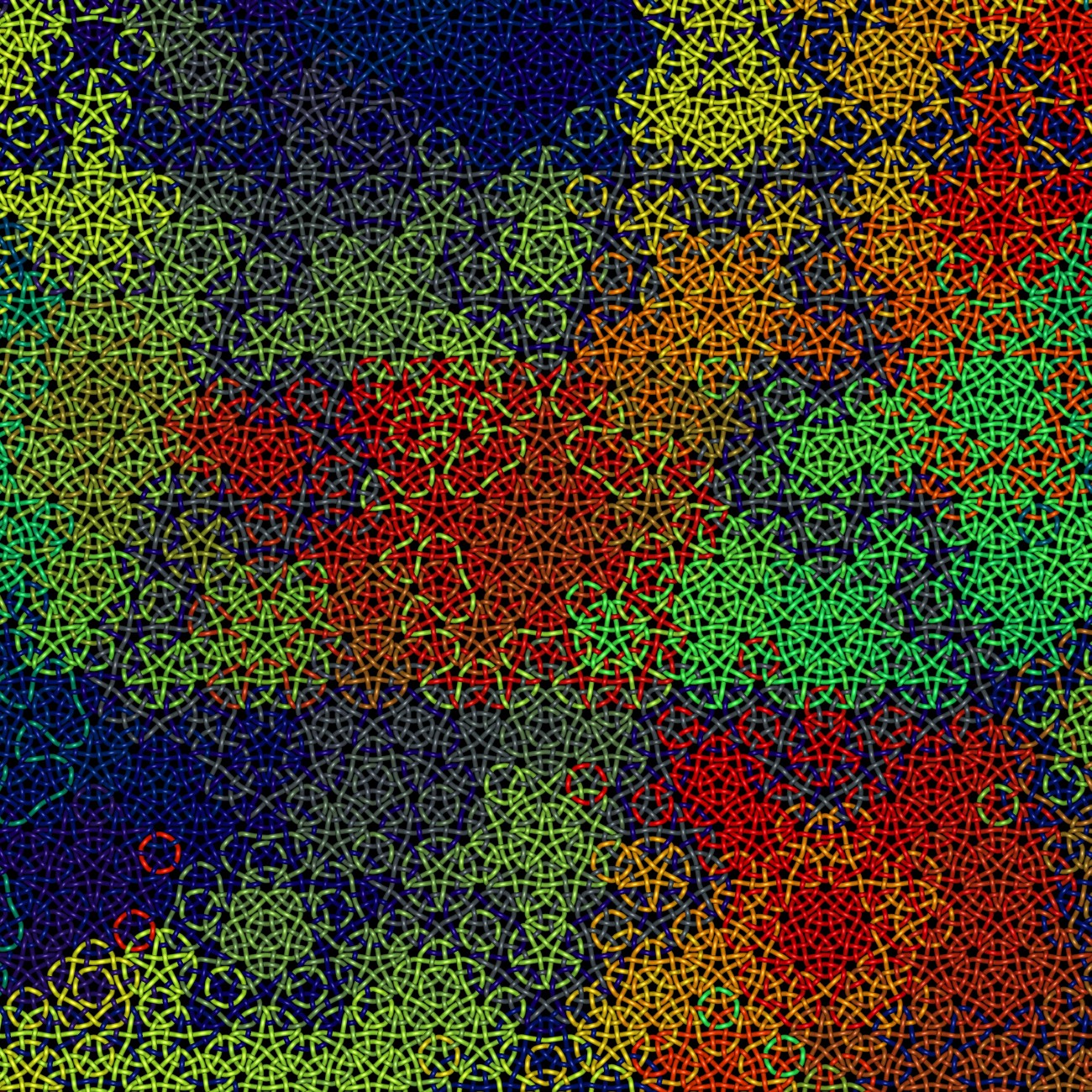
knot tiling — Computer generated weaving as decorative art. image source

This image shows the modern approach of possibilities on the subject of weaving. Note that many of the threads are closed circles, as links. A weaving made of entirely links is not explored in knitting, fabric, or any sort of weaving artifact, simply because it is not practical. However, as modern material science, this is a new vista. Or as mathematical classification of weaving, this have not been studied much, if at all.

Also, when we consider the math aspects of links, knots, weavings, we think of topology. That is, how each thread or inter-woven with other threads. However, weavings as a decorative art, the geometric positioning, is a critical part of the work.

Hyperbolic Surface Crochet

Unrelated to math aspects of weaving, but saw this the other day. Knitting a hyperbolic surface.

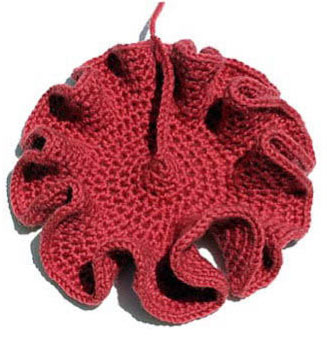
crochet hyperbolic surface — Knitting that forms a hyperbolic surface. [image source http://www.theiff.org/oexhibits/oe1e.html ]

Actually, the person who knitted this is Daina Taimina, a mathematician, and she has written a book. Crocheting Adventures with Hyperbolic Planes 2009, by Daina Taimina. Buy at amazon

Little Math Research

As far as i know there's not much serious mathematical study on knitting, Chinese knots, weaving, as a math subject. By that, i mean, definition, analysis, theories, of weaving from a professional mathematician, as a sub-field of combinatorial geometry, on what weaving are possible, their classification, etc. Not, for example, studies on how to create such work, or survey of abstract patterns on existing artworks, from artisans or artists or anthropologists, or algorithms about how to create such patterns by computer programers.

I've only seen some research papers by Branko Grünbaum and G C Shephard on the weaving studies. e.g. A Catalogue of Isonemal Fabrics 1985, Branko Grünbaum and G C Shephard, “Discrete Geometry and Covexity” vol 440.

[see Tilings and Patterns Book]