Equiangular Spiral
History
The investigation of spirals began at least with the ancient Greeks. The famous Equiangular Spiral was discovered by Rene Descartes, its properties of self-reproduction by Jacob Bernoulli (1654 to 1705) (aka James or Jacques) who requested that the curve be engraved upon his tomb with the phrase “Eadem mutata resurgo” (“I shall arise the same, though changed.”) [Source: Robert C Yates (1952)]
The equiangular spiral was first considered in 1638 by Descartes, who started from the property s = a.r. Evangelista Torricelli, who died in 1647, worked on it independently and used for a definition the fact that the radii are in geometric progression if the angles increase uniformly. From this he discovered the relation s = a.r; that is to say, he found the rectification of the curve. Jacob Bernoulli, some fifty years later, found all the “reproductive” properties of the curve; and these almost mystic properties of the “wonderful” spiral made him wish to have the curve incised on his tomb: Eadem mutata resurgo: “Though changed I rise unchanged”. [source: E H Lockwood (1961)]
Description
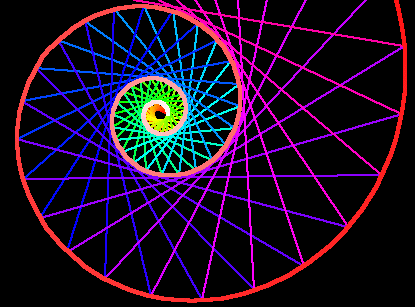
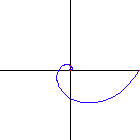
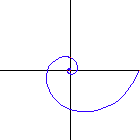
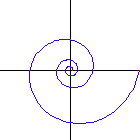
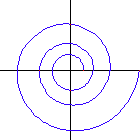
Equiangular spiral describes a family of spirals of one parameter. It is defined as a curve that cuts all radial line at a constant angle.
It also called logarithmic spiral, Bernoulli spiral, and logistique.
Explanation:
- Let there be a spiral (that is, any curve r==f[θ] where f is a monotonic inscreasing function)
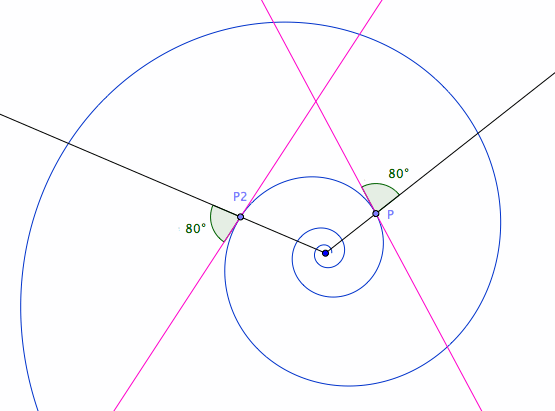
- From any point P on the spiral, draw a line toward the center of the spiral. (this line is called the radial line)
- If the angle formed by the radial line and the tangent for any point P is constant, the curve is a equiangular spiral.
A special case of equiangular spiral is the circle, where the constant angle is 90°.
Formula
Let α be the constant angle.
Polar: r == E^(θ * Cot[α])
Parametric: E^(t * Cot[α]) {Cos[t],Sin[t]}
Cartesian: x^2 + y^2 == E^(ArcTan[y/x] Cot[α] )
Properties
Point Construction and Geometric Sequence
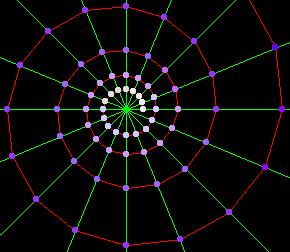
Length of segments of any radial ray cut by the curve is a geometric sequence, with a multiplier of E^(2 Pi Cot[α]).
Lengths of segments of the curve, cut by equally spaced radial rays, is a geometric sequence.
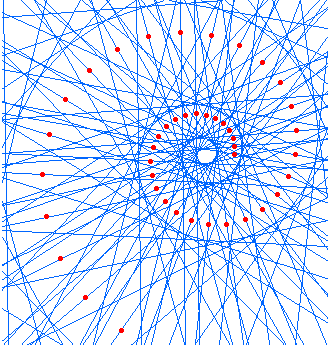
Catacaustic
Catacaustic of a equiangular spiral with light source at center is a equal spiral.
Proof: Let O be the center of the curve. Let α be the curve's constant angle. Let Q be the reflection of O through the tangent normal of a point P on the curve. Consider Triangle[O,P,Q]. For any point P, Length[Segment[O,P]]==Length[Segment[P,Q]] and Angle[O,P,Q] is constant. (Angle[O,P,Q] is constant because the curve's constant angle definition.) Therefore, by argument of similar triangle, then for any point P, Length[Segment[O,Q]]==Length[Segment[O,P]]*s for some constant s. Since scaling and rotation around its center does not change the curve, thus the locus of Q is a equiangular spiral with constant angle α, and Angle[O,Q,P] == α. Line[P,Q] is the tangent at Q.

Curvature
The evolute of a equiangular spiral is the same spiral rotated.
The involute of a equiangular spiral is the same spiral rotated.

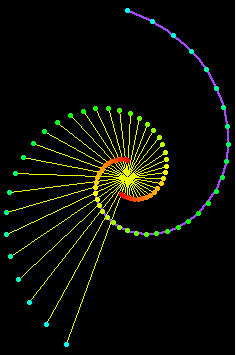
Radial
The radial of a equiangular spiral is itself scaled. The figure on the left shows a 70° equiangular spiral and its radial. The figure on the right shows its involute, which is another equiangular spiral.
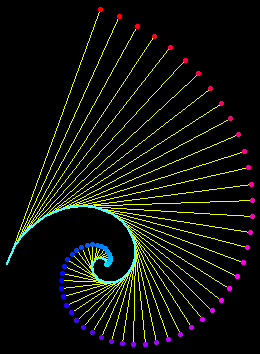
Inversion
The inversion of a equiangular spiral with respect to its center is a equal spiral.
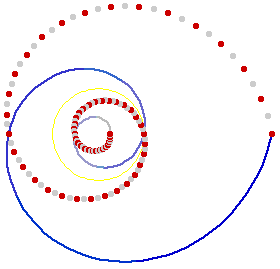
Pedal
The pedal of a equiangular spiral with respect to its center is a equal spiral.
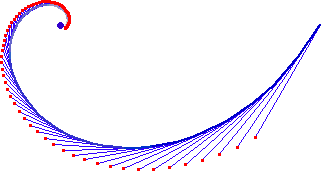
Pursuit Curve
Persuit curves are the trace of a object chasing another. Suppose there are n bugs each at a corner of a n sided regular polygon. Each bug crawls towards its next neighbor with uniform speed. The trace of these bugs are equiangular spirals of (n-2)/n * Pi/2 radians (half the angle of the polygon's corner).
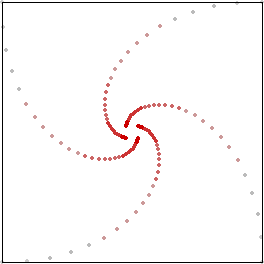
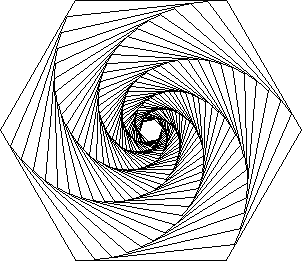
Spiral in nature
Spiral is the basis for many natural growths. Seashells have the geometry of equiangular spiral.

Related Web Sites
- Mathematica Packages for Plane Curves
- Curves and Their Properties: Spiral, p206
- https://mathshistory.st-andrews.ac.uk/Curves/Equiangular/
- Khristo Boyadzhiev, Spirals and Conchospirals in the Flight of Insects. The College Mathematics Journal, Jan 1999. Khristo_Boyadzhiev_CMJ-99.pdf
 Math of Seashell Shapes
Math of Seashell Shapes