Evolute
Mathematica Notebook for This Page .
History
Studied by Huygens in 1673.
Description
Evolute is a method of deriving a new curve based on a given curve. It is the locus of the centers of tangent circles of the given curve.
Evolute of a ellipse.
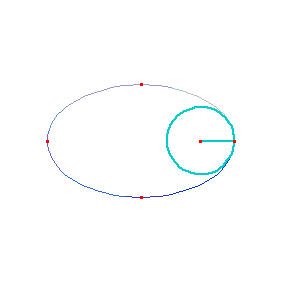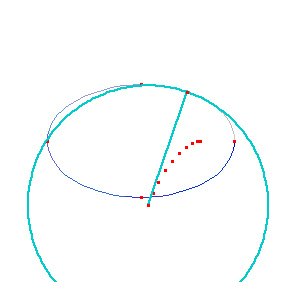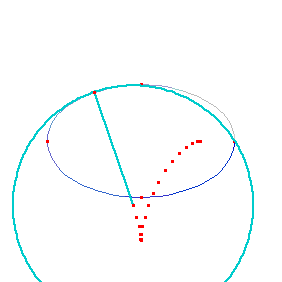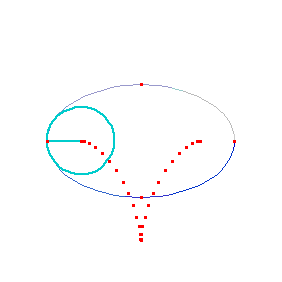
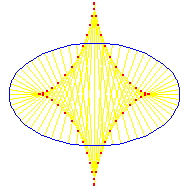
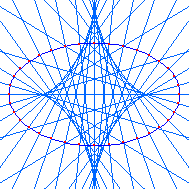
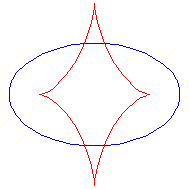
Formula
Given a curve in parametric form {x[t], y[t]}, its evolute is
{x + (y'*(x'^2 + y'^2)) / ( y'*x'' - x'*y''),
y + (x'*(x'^2 + y'^2)) / (-(y'*x'') + x'*y'')}
Properties
Parallels and Evolute
Theorem: The locus of Cusps of a curve C's parallel curves is the evolute of C. This is a alternative definition of evolute. See the Parallel page.
Evolute and Involute
If curve A is the involute of curve B, then curve B is the evolute of curve A. The converse is true locally, that is: If curve B is the evolute of curve A, then any part of curve A is the involute of some parts of B.
Curves relations by evolute and involute
| Base Curve | Evolute |
|---|---|
| cardioid | cardioid scaled by 1/3 |
| nephroid | nephroid 1/2 |
| astroid | astroid 2 |
| deltoid | deltoid 3 |
| epicycloid | epicycloid |
| hypocycloid | hypocycloid |
| cycloid | cycloid |
| Cayley's sextic | nephroid |
| parabola | semicubic parabola |
| limacon of Pascal | catacaustic of a circle |
| equiangular spiral | equiangular spiral |
| tractrix | catenary |
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .