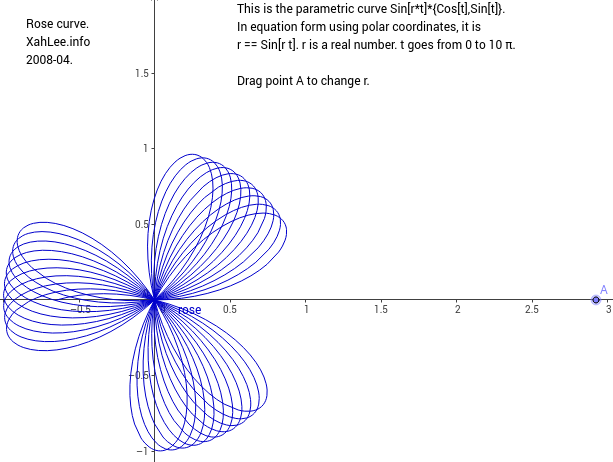
Rose Curve
History
Studied by Guido Grandi around 1723.
aka rhodonea
Description
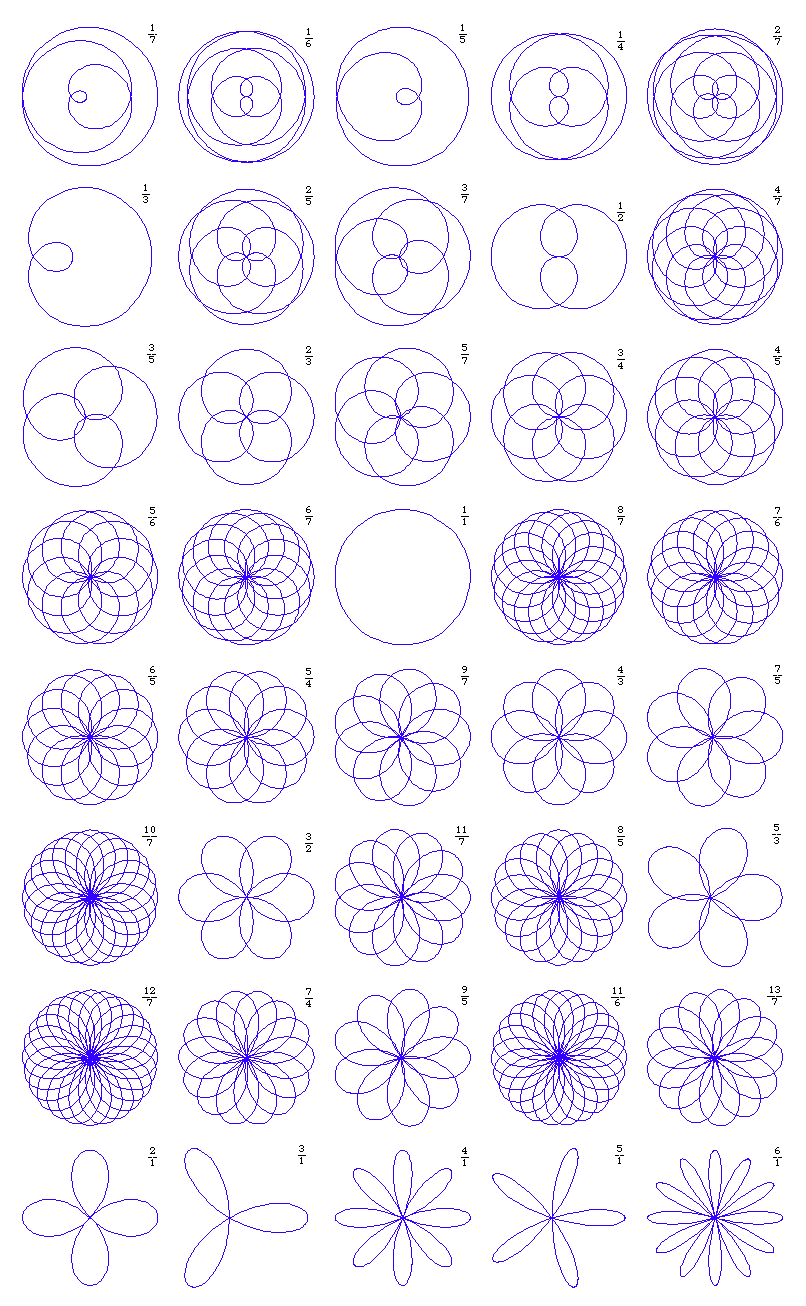
Rose describes a family of curves. Roses are probably historically defined as the pedals of epi/hypocycloids with respect to their centers, which has the polar form r==Cos[p/q*θ], where p and q are relatively prime. Not all possible rational p/q in r==Cos[p/q*θ] occur as pedals of epi/hypocycloids, but we can define rose to be the curve r==Cos[p/q*θ], where p/q is any rational. The curve has loops that are symmetrically distributed around the pole. The loops are called petals or leafs.
If p and q are both odd, it has a period of Pi*q with p petals, otherwise the period is 2 Pi*q and has 2*p petals. In particular, r==Cos[p/1*θ] has p petals and periodicy Pi if p is odd, else it has 2*p petals with period 2 Pi. The period of the curve can be derived by studying the period of the parametric form Cos[p/q*t]*{Cos[t],Sin[t]}. In particular, analying the period of Sin[p/q*t]*Sin[t]. Similarly, the number of petals can be inferred. The curve r==Cos[r*θ] where r is irrational, is non-periodic.
Roses are shaped like a airplane propeller when q==1. If q is not 1, the “propeller blades” are fat and overlap, which alludes to its name “rose”.
The rose r==Cos[3*θ] is called Trifolium (having 3 petals), and r==Cos[2*θ] is called Quadrifolium (having 4 petals). The pedals of a deltoid with respect to one of its cusp, vertex, or center is called a folium, bifolium, and trifolium respectively. They are called n-foliums because the curves have n loops. However, folium and bifolium are not roses. Only the trifolium is a rose. (*XahNote: verify if the curve historically called “folium” is the 1 petalled rose r==Cos[1/3*θ].*)
Formula
Polar equation: r==Cos[p/q*θ].
Cartesian equation for a 4-pedaled rose r==Cos[2*θ] rotated by 2 Pi/8 is (x^2+y^2)^3==4*x^2*y^2.
list all equation in rect coord for n-leafed rose. Proof if for some n its not algebraic.
Properties
Rose as Hypotrochoid
Roses are special cases of hypotrochoids. (See: Curve Family Index)
Roses are probably also epitrochoids. Prove or disprove it. Also, epitrochoid and or hypotrochoids has double generation; check how it applies to rose.
Pedal, Radial, Epycycloid, and Hypocycloid
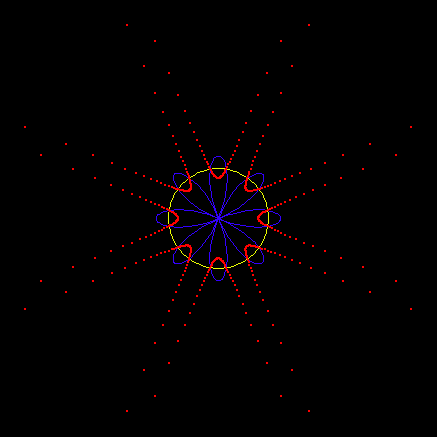
The pedal and radial of a epi/hypocycloid with respect to their centers are roses. The following image epiHypocycloidEpiPedal.png shows 40 epicycloids (blue) and their pedals (red). See epi/hypocycloid page for more detail and illustration.
“Real” roses
Cotes's Spiral
Rose inverts to a curve called Cotes's Spiral.