Cross-Cap Surface

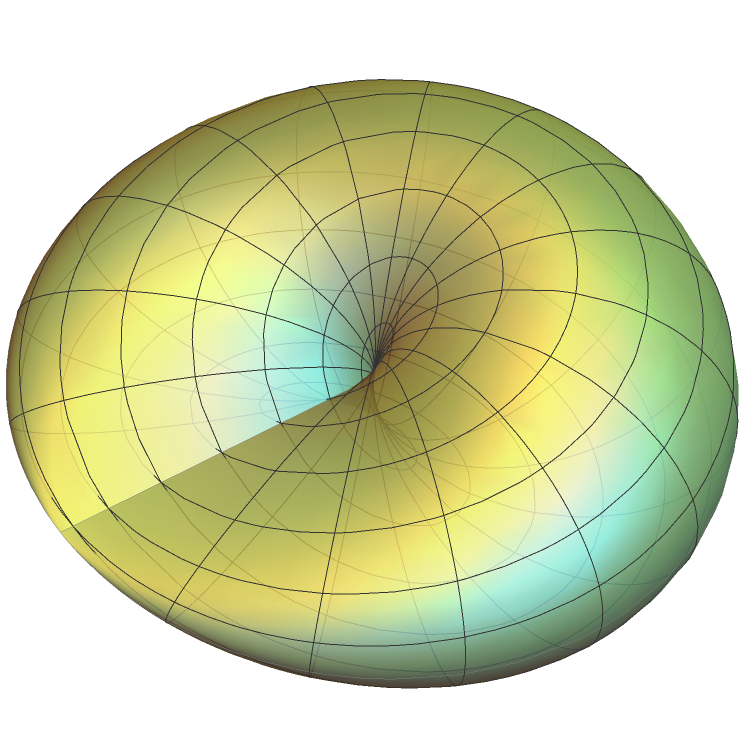
cross-cap t5hFb
cross-cap 
ParametricPlot3D[
 {(Sin[u]*Sin[2*v]/2), (Sin[2*u]*Cos[v]*Cos[v]), (Cos[2*u]*Cos[v]*
    Cos[v])}, {u, 0, Pi}, {v, 0, Pi}, Boxed -> False, Axes -> False,
 BoundaryStyle -> {Thin, Gray}, PlotPoints -> 20, MaxRecursion -> 4,
 PlotStyle ->
  Directive[RandomColor[], Opacity[.8], Specularity[1, 20]]]

The Cross-cap is a representation of the projective plane. (A “projective plane” is a plane with a line added at infinity. It developed out of study of projective geometry.)

Cross-cap is like a shrinked Torus where there is no middle hole and the side has been pinched together in such way that the top cross to the bottom.

One way to think of cross-cap is as a hemi-sphere (or a bowl), and imagine each point on the rim is connected to points on opposite side.

One way to think of cross-cap is, draw a filled circle on paper, and imagine each point on the rim is connected to the point on the opposite side.

The significance of this surface is that it gives us a visual guide of the topology of the real projective plane. 〔see Intro to Real Projective Plane〕

Other surfaces immersed in 3D that are topologically equivalent to the projective plane are: