Extending the Euclidean Plane: Riemann Sphere and Real Projective Plane
Riemann Sphere
take a plane, add a “point at infinity”, such that, starting from the origin and going in any direction in the plane will pass this “point at infinity” and return from the other direction. This abstract surface is called Riemann sphere.
The Riemann sphere is best visualized by Stereographic Projection.
Riemann sphere is fundamental in complex analysis. See also: Geometric Transformation on the Plane .
Real Projective Plane
take a plane, add a “line at infinity”, the result is called “real projective plane”.
Another way to think of this is, take a plane, and like before, starting from the origin we go in a direction, and pass a “point at infinity” and return from the other side. But, if we start in another direction, we pass a different “point at infinity” and return from the other side. So, each direction has a “point at infinity”.
“real projective plane” is topologically equivalent to Cross-Cap Surface .
Real Projective Plane in fundamental in studying projective geometry, which is a branch of geometry.
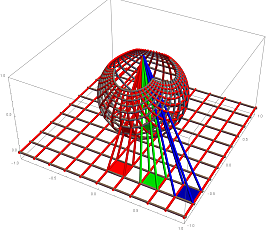 Stereographic Projection
Stereographic Projection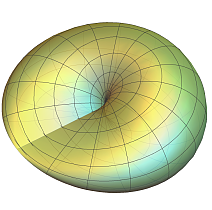 Cross-Cap Surface
Cross-Cap Surface