What is Technical Drawing, Descriptive Geometry, Projective Geometry, Linear Algebra

This page discusses the relations between Technical Drawing, Descriptive Geometry, Projective Geometry, Linear Algebra, and CAD.

Technical Drawing and Descriptive Geometry

In the early 1990s, when i was in my early twenties, i was fascinated by Technical drawing. Technical drawing is those you see in wire frame cars, architecture blue-prints, mechanical devices designs, etc. This skill fascinated me. In college, you can major in technical drawing and become a draftsman.

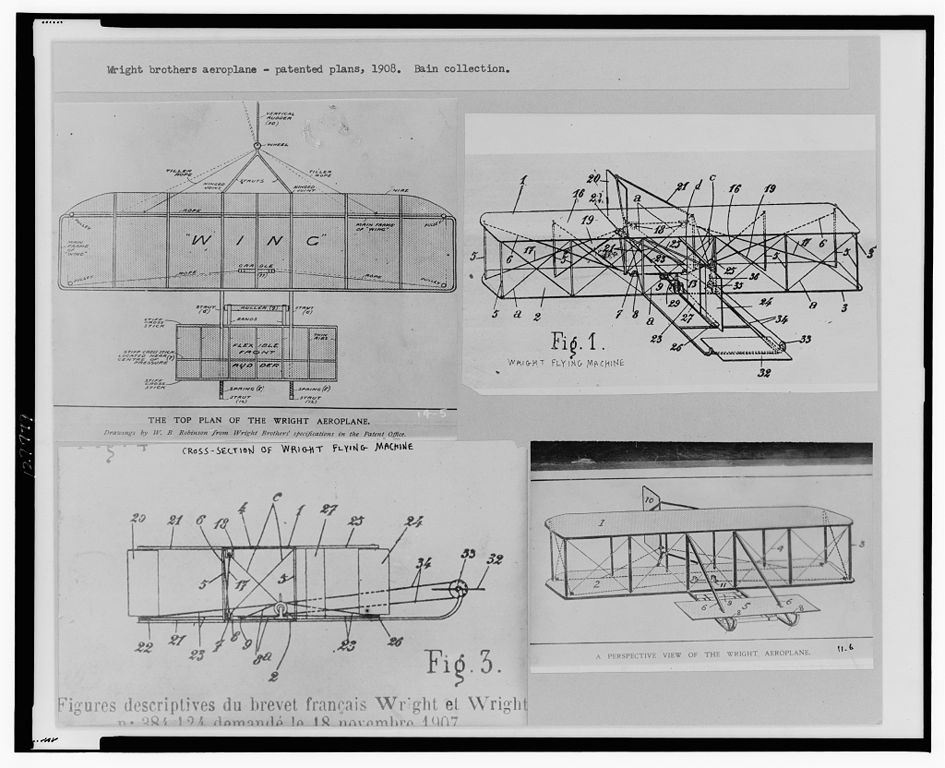
Technical drawing is a skill, a vocation, but today it is much replaced by operating Computer-aided design (CAD) software. (for example, AutoCAD, SketchUp, and many others. See: List of 3D Modeling Software.)

Descriptive Geometry = Principles of Technical Drawing

The techniques, methods, principles, of technical drawing, is called Descriptive Geometry.

Suppose there is a ashtray on a table. Now, you are to draw this ashtray. Could you, sketch a drawing, so that, when your drawing is placed on top of a photograph of it, they match exactly?

Descriptive geometry, is the engineering discipline that helps you draw pictures correctly.

The name “descriptive geometry” might seems to mean it's some study of geometry, but actually it is not a study of math or geometry. A better name would be “principles of technical drawing”.

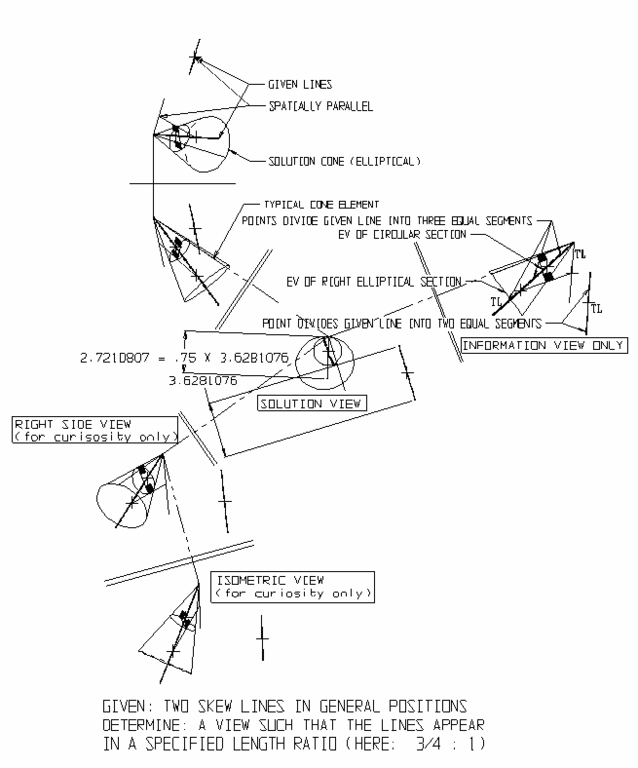
Projective Geometry

Now, the gist of technical drawing is just linear projection. That is, project points in 3D space into a 2D paper, in such a way it is realistic. This is basically how our eye works. Light from 3D space come into our pupil and is projected back onto our 2D retina.

The theoretical aspects in projection, is known as projective geometry. It is concerned about, for example, what properties are invariant under projection. Projective geometry, is indeed, a major branch of math. However, due to the nature of projective geometry, it has no practical connection to technical drawing.

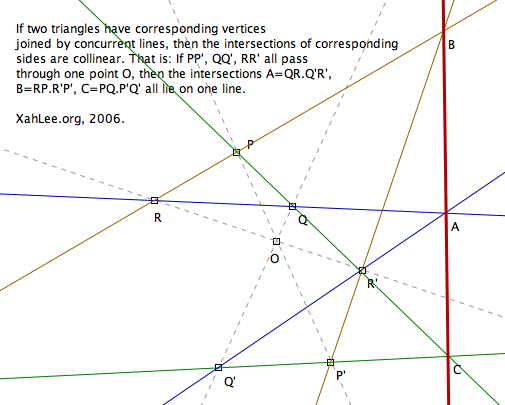
For example, one of the most important theorem in projective geometry is called Desargues's Two Triangle Theorem. It basically states how any 2 triangles's sides and the corners, when connected in a certain way, always meet in a single point or on a single line. For more about the subject, see: Introduction to Real Projective Plane.

Linear Algebra

Another subject intimately related to descriptive geometry and projective geometry is linear algebra.

Linear Algebra, is a branch of math that has application in geometry. In our context, it lets you compute the exact coordinates of a point in space on a given plane with a given camera position.

Before our digital computer era, when a technical draftman wants to draw something, he uses principles in Descriptive Geometry, with tools like T-square , compass, and drafting table. In modern days of computing, Descriptive Geometry is becoming little used, because we can now compute the exact coordinates of points in the scene and their projection on the plane, directly, using computer and linear algebra, and thus bypassing those indirect mathematical rules and principles of how to do drawing correctly.

This direct computation of coordinates, is part of linear algebra. In particular, matrix multiplication. So, in CAD software, it is the matrix multiplication that is at play, with results that is more direct and perfectly accurate than the nature of descriptive geometry. Note that, this is only possible with massive computing power.

Summary

• The nature of Technical Drawing is drawings made by Linear Projection.
• Descriptive Geometry is a collection of guides and principles on how to accurately do technical drawing. This is before the time of modern computers with CAD software.
• Projective Geometry is a branch of mathematics that studies some properties about projection. The motivation of projection geometry began when graphics artists in the 1600s discovered the technique of perspectivity that lets them create drawings that have a realistic, 3D sense (as opposed to being flat). However, Projective Geometry quickly developed into a pure, abstract mathematics, having absolutely nothing to do with drawings or its technique.
• Linear Algebra is a branch of mathematics that studies some properties that originates from linear polynomials. In particular, one of its main application is to determine the exact coordinates from linear projection (matrix multiplication). This is how CAD software is able to compute the coordinates of 3D models for displaying on the 2D screen.