Stereographic Projection 3D-Printed Physical Model
Stereographic Projection and mobius transformation. If you want to understand Einstein's theory of relativity, you must understand mobius transformation. To understand mobius transformation, you must first understand Riemann sphere, complex numbers, geometric inversion.


- https://youtu.be/VX-0Laeczgk
- Stereographic projection by Henry Segerman
- http://www.segerman.org/
Moebius Transformation

- https://youtu.be/0z1fIsUNhO4
- Moebius Transformations Revealed
- by Douglas Arnold and Jonathan Rogness.
In these videos, can you see that, the plane, and sphere, are mapped. That is, each point on the plane has a corresponding point on the sphere, and vice versa (except the north pole of the sphere, which should map to some “infinite” point on the plane)
Now, this idealized plane, with a point at infinity in the stereographic projection sense, is called Riemann sphere. Riemann sphere is a plane, but it has the word “sphere” in it because the essence of this plane is really a sphere, as you see in the videos. You can think of it as a plane or a sphere.
In the video, you see a grid on the plane and it gets mapped to the sphere. Now, if you only look at the sphere, and think of the sphere as a plane, then, you see that the lines from the grid become arcs of circles. There is a function in math that does exactly that transformation. It's called geometric inversion.
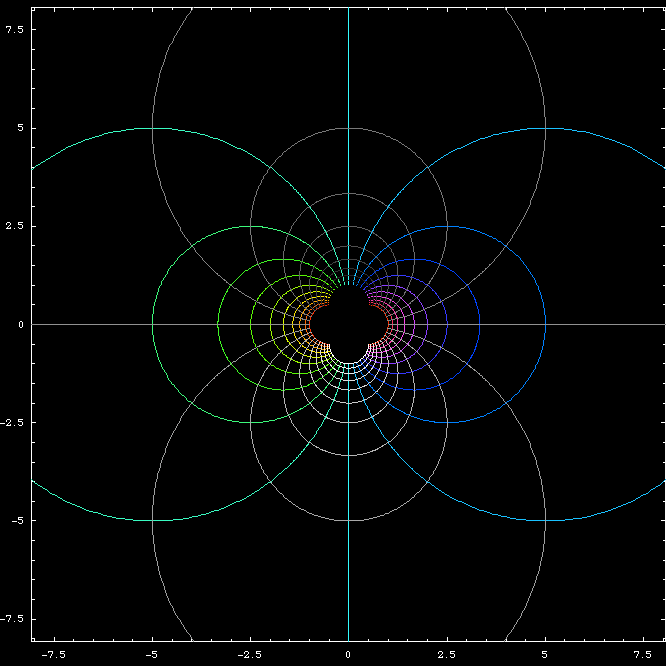
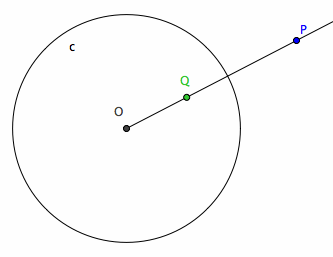
Inversion in geometry is a transformation. Let P be a given point. Let c be a circle centered on O and radius r. The inverse of P with respect to c is a point Q on the line[O,P] such that distance[O,P] * distance[O,Q] == r^2.
Geometric inversion is fascinating. It is like a mirror that warps the plane inside out. And, line become circle, and circle become line. For more pictures, see: Geometric Inversion .
If you combine {geometric inversion, rotation, translation, reflection} into one function, that function is called Möbius transformation. And the formula/definition of this function, expressed with complex numbers, is f[z]:= (a*z+b)/(c*z+d) with a*d - b*c ≠ 0.
more examples of Mobius Transformations, see: Mobius Transformations
The Mobius transformation function, and the Riemann sphere, are all expressed in complex numbers. At this point, you might think, it's too complicated. The name “complex number” is too bad, but the idea of complex number, is really easy to understand. It is simply a 2D vector plane with the idea of rotation operation between 2 vectors. So, you actually don't need complex numbers, but using complex number just make the formula of rotation simpler.
In the same sense, that you don't really need exponential function such as (2^3 = 8), because it's just repeated multiplication (2*2*2=8), but you don't really need multiplication neither, because it's simply repeated addition (2*3= 2+2+2, so, (2*2)*2 is (2+2)+(2+2), and is 2^3). But the concept of multiplication, and exponentiation, make things a lot simpler.
In a similar way, complex number makes rotation of 2D vector much simpler. For a easy-to-understand intro of geometric interpretation of complex numbers, see: Coordinate Transformation
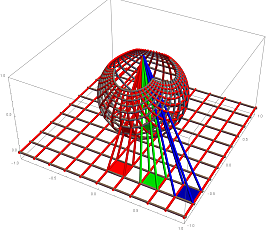 Stereographic Projection
Stereographic Projection