A point {a,b} has a distance to the origin. Also, it makes a angle with the positive x-axis if we consider the line {0,0} to {a,b}. These two concepts are very useful and convenient, that we define the length of a point to be the distance from the origin to the point, and we define the angle of a point to be the angle it makes with the positive x-axis. When a point is considered this way, we call it a vector. We say, that a vector has a length, and a angle.
Vector A, with angle α and length r.
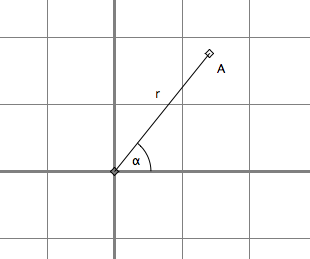
If a point A has coordinates {a,b}, its length can be expressed as Sqrt[a^2+b^2]. This comes easily from Pythagorean theorem.
The angle of a vector {a,b} is ArcTan[b/a]. This is from trigonometry.
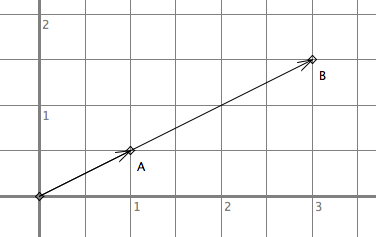
Given a vector {a,b}, to scale (expand/shrink) the vector by s around the origin, the new vector is {a,b}*s.
A vector A:={1,0.5} scaled by 3 with new coordinate B:={3,1.5}.
Let
f[x,y]==0
be the equation for a curve in rectangular coordinates.
To scale the curve by s, the new equation would be:
f[x/s, y/s]==0.
Let
f[θ,r]==0
be the equation for a curve in polar coordinate.
To scale it by s, the new formula is
f[r/s,θ]==0
Let
{f[t],g[t]}
be the parametric formula for a curve in rectangular coordinate.
To scale it by s, the new formula is
{f[t],g[t]}*s
Let
{f[t],g[t]}
be the parametric formula for a curve in polar coordinate.
To scale it by s, the new formula is
{f[t]*s,g[t]}
A circle centered {1,0} with radius 1, and it scaled by a factor of 1/2.
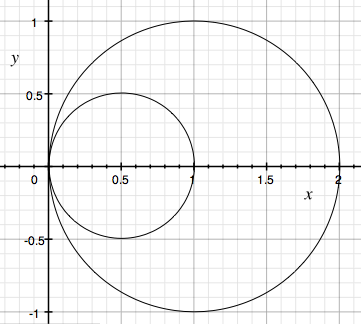
A circle (x-1)^2+y^2-1==0 has center {1,0} and radius 1. To scale it by a factor of 1/2, we replace x by 2*x and y by 2*y, to obtain (2*x-1)^2+(2*y)^2-1==0.
Given a vector {a,b}, to translate the vector by {c,d}, the new vector is {a+c,b+d}.
The adding of coordinate components is a very convenient operation. We define it as vector addition. That is, {a,b}+{c,d} := {a+c,b+d}, and its geometric interpretation is that one vector is moved to a new position by the second vector.
Vector A plus vector B, resulting in vector C. Geometrically, C is the vector A moved by B, or vice versa. The 3 vectors and the origin always forms a parallelogram. Vector Addition
Let
f[x,y]==0
be the equation for a curve in rectangular coordinates.
To translate the curve by vector {a,b}, the new equation would be:
f[x-a, y-b]==0.
Let
{f[t],g[t]}
be the parametric formula for a curve in rectangular coordinate.
To translate it by vector {a,b}, the new formula is
{f[t],g[t]} + {a,b}
The point {Cos[α],Sin[α]} is a point with α angle with the positive x-axis and 1 unit distant from the origin. To rotate it by angle β, then new coordinate is {Cos[α+β],Sin[α+β]}. By trig identity of double angle:
Cos[a+b] == Cos[a] Cos[b] - Sin[a] Sin[b] and Sin[a+b] = Cos[a] Sin[b] + Cos[b] Sin[a]
, we can be write our rotated point as
{Cos[α] Cos[β] - Sin[α] Sin[β],
Cos[α] Sin[β] + Cos[β] Sin[α]}
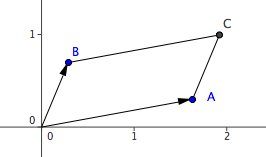
Now, look at the components in the above coordinate. They are of the form Sin[] or Cos[]. In other words, if we have a point A := {Cos[α],Sin[α]} and point B := {Cos[β],Sin[β]}. Then, the point A rotated by β angles can be written in terms of the coordinate components of A and B.
In other words, if A is {a,b} and B is {c,d} and suppose both are 1 unit distant from the origin, then a new point C, obtained by rotating A by B's angle, can be expressed in terms of coordinate components of A and B by this expression: {a c-b d, a d+b c}.
But now if we substitute a by r*a and b by r*b and c by s*c and d by s*d. In other words, we start with points {r a,r b} which is r distant to the origin, and point {s c,s d} which is s distant. Then, the above formula gives us {r s (a c-b d), r s (a d+b c)}. From this, we can say that length of the new vector is just the product of the lengths of the old vectors.
In summary, if A is {a,b} with angle α and length r, and B is {c,d} with angle β and length s, then {a c-b d, a d+b c} is a point with angle α+β and length r*s.
This formula is extremely powerful, because it lets us do rotation and scaling around the origin at the same time, and by simply using another vector.
Let f[x,y]==0 be the equation for a curve in rectangular coordinates.
Suppose we want to rotate it by a angle θ. First, we find a vector {c,d} of distance 1 having angle -θ, which is {Cos[-θ], Sin[-θ]}. Then, we do this substitution into the function:
x → x c - y d y → x d + y c so we obtain: f[x c - y d, x d + y c]
This would be the new curve we wanted. If the vector {c,d} has length r, then the new curve would be dilated by 1/r.
A circle rotated and shrinked around the origin.
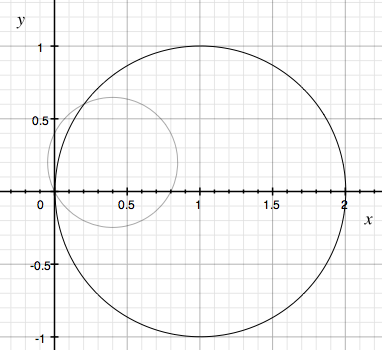
Suppose: f[x,y] := (x-1)^2+y^2-1
Then, f[x,y]==0 is a circle centered on {1,0} with radius 1. Let's say we want to rotate it by angle θ represented by the vector {2,1}. So, we should use a vector that has angle -θ, which is {2,-1}. So, {c,d}:={2,-1}. Now, we substitute the rotation with our formula
x → x 2 - y (-1) y → x (-1) + y 2
So our new function is:
g[x,y] := ((x 2 - y (-1))-1)^2 + ( x (-1) + y 2)^2-1
Then, g[x,y]==0 is our old circle rotated. Note that it is also shrinked. This is because the vector we used {2,-1} has a length greater than 1. If we want to keep the circle the same size, we should use a vector with length 1, which is {Cos[-θ],Sin[-θ]}
Let
f[r,θ]==0
be the equation for a curve in polar coordinate.
To rotate it by α, the new formula is
f[r,θ-α]==0
Let
{f[t],g[t]}
be the parametric formula for a curve in rectangular coordinate.
To rotate the curve by θ radian, the new formula is
{Cos[θ]*f[t] - g[t]*Sin[θ], Cos[θ]*g[t] + f[t]*Sin[θ]}
or, if {c,d} is a unit vector with θ radians,
the new rotated curve expressed in terms of {c,d} is
{f[t]*c-g[t]*d, f[t]*d+g[t]*c}.
Let
{f[t],g[t]}
be the parametric formula for a curve in polar coordinate.
To rotate the curve by θ, the new formula would be:
{f[t],g[t]+θ}
blog comments powered by Disqus