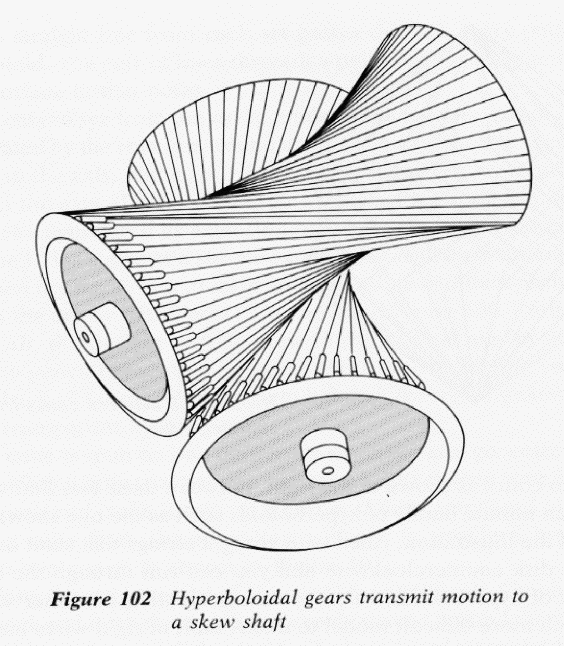
Hyperboloid of One Sheet

The hyperboloid Of One Sheet is a surface of revolution of the curve family hyperbola

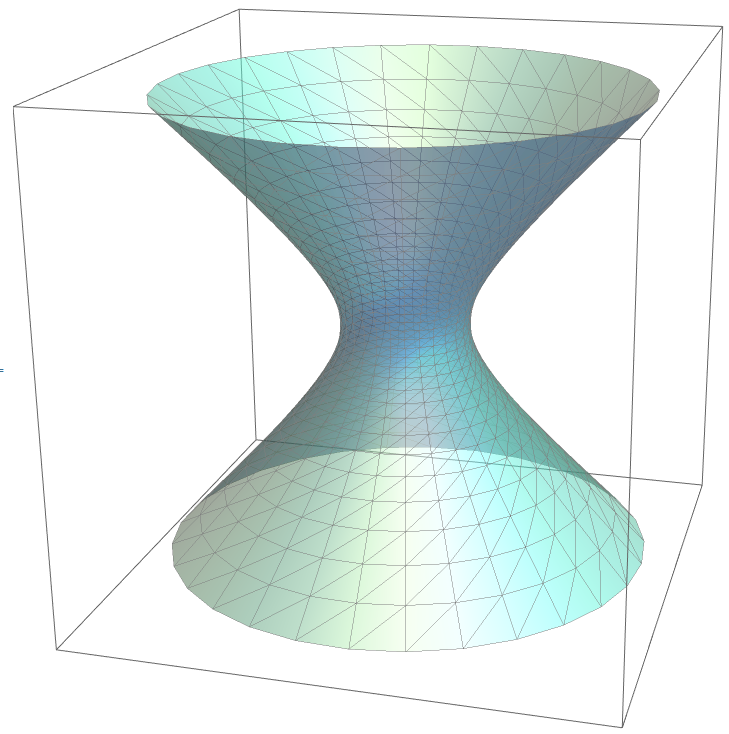
hyperboloid 1 C2xyn
hyperboloid 1 
ParametricPlot3D[{Cosh[u]*Cos[v], Cosh[u]*Sin[v], Sinh[u]}, {u, -2, 2}, {v, 0, 2*Pi},
  PlotPoints -> 30, MaxRecursion -> 0, Mesh -> All, Boxed -> True, Axes -> False,
  BoundaryStyle -> {Thin, Black}, MeshStyle -> {Gray},
  PlotStyle -> Directive[RandomColor[], Opacity[0.5], Specularity[1, 20]]]

Ruled Surface

A revolving around its transverse axis forms a surface called “hyperboloid of one sheet”. A hyperboloid is a Ruled Surface.

Ruled surfaces are surfaces that for every point on the surface, there is a line on the surface passing it. Or, in other words, a surface generated by a line. If for each point on the surface there are two lines on the surface passing it, then it's called doubly-ruled surface. Hyperboloid is a doubly-ruled surface.

Ruled surfaces also include cylinder and helicoid. There are only 3 doubly ruled surfaces: • Hyperboloid of One Sheet • Hyperbolic Paraboloid • plane.

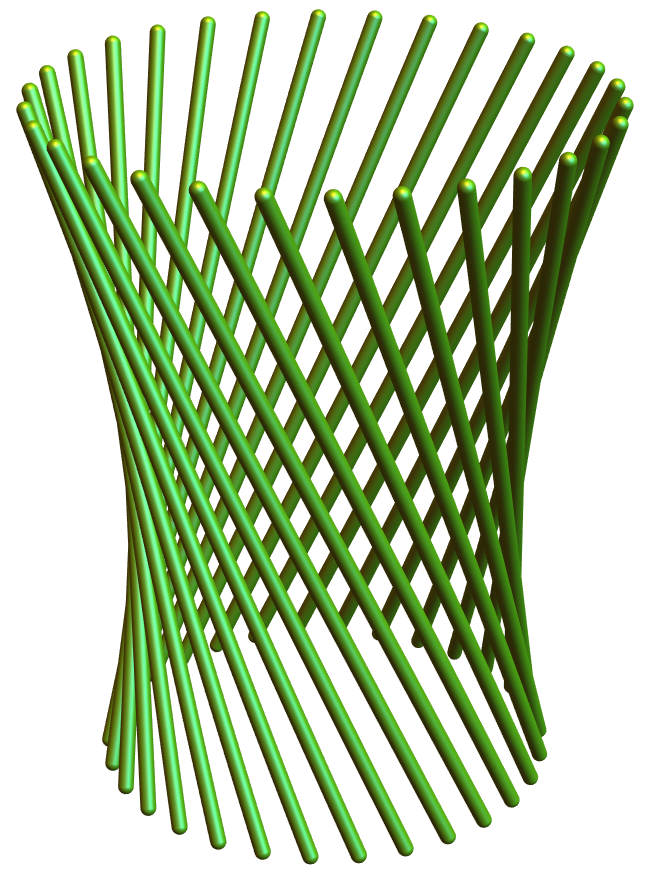
hyperboloid 1 sheet gCC9K hyperboloid 1 sheet 7xdwv hyperboloid 1 sheet sJhPY hyperboloid 1 sheet JMTtp
hyperboloid 1 sheet 
barLength = 2;
offSet = 0.5;
girth = 1;
tiltLevel = 45*Degree;
numberOfTubes = 30;
oneTube = Rotate[Tube[{{0, 0, -barLength + offSet}, {0, 0, barLength + offSet}}], tiltX, {1, 0, 0}];
Table[Graphics3D[{RandomColor[], Specularity[1, 20], Table[Rotate[Translate[oneTube, {girth, 0, 0}],
      n*Degree, {0, 0, 1}], {n, 0, 360, 360/numberOfTubes}]}, Boxed -> False, Axes -> False,
   ViewPoint -> {2, 0, 1}, PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}],
  {tiltX, 10*Degree, 70*Degree - 10*Degree, (70*Degree - 10*Degree)/4}]
hyperboloid sculpture
Two hyperboloid sculptures. The left can be made into a modern fruit basket, and the right a paper waste basket. (source: Second Life gallery)
hyperbolic basket2
Basket modeled by hyperboloid. [from www.momastore.com 2001]

Spinning Cube Silhouette

The silhouette of a rotating dice is a hyperbola.

spinning cube
A sculpture emulating a spinning cube. (source: Second Life gallery)
spinning dice photo
spinning dice
polyhedra dices
polyhedra dice
Stick thru curved hole toy. [Source http://www.thingiverse.com/thing:1729011]

Hyperboloid in Architecture

James S McDonnell Planetarium
The James S McDonnell Planetarium building at the St. Louis Science Center.
Kobe port tower d75b4-s500
The Kobe Port Tower. 2142×3200 [image source]

For more photos, see: Hyperboloid Architecture

hypoid
Hyperboloid can be used for gear surface, called a Hypoid. (Source: Penrose Tiles to Trapdoor Ciphers by Martin Gardner. Buy at amazon, chapter 15).

Conic Section Surfaces