Xah Talk Show 2025-04-20 Ep645 Wolfram language, physics emulation of bouncing balls

physics bouncing balls

how to program this?

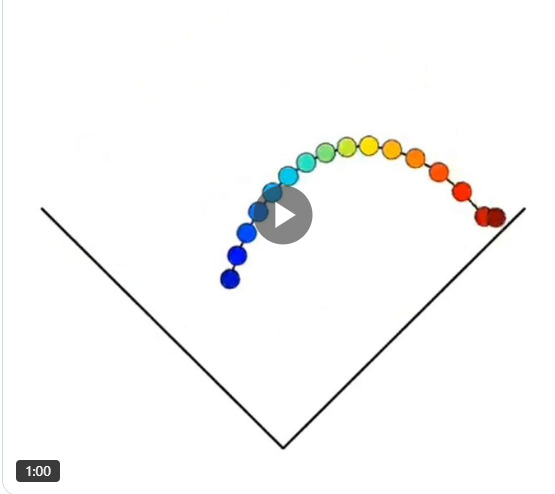
https://x.com/shitpost_2077/status/1913510379491131831

analysis of what it is doing

haven't done anything like this. but first, you need to consider what it is doing.

look at first 2 balls. seems their distances gets apart.

now look at just first ball. seems it always follow the same path back and forth. now look at just last ball. same

so it seems, each ball, always travels in the exact same path.

does a ball's speed change? watch a ball from animation begin to end. seems no.

do they have different speed? look at the first ball and last. top ball moves much faster. so, each ball have different speed. top fastest, bottom slowest.

so now it seems simple. so there is nothing about emulating physics. it's just plain geometry.

what exact path is it? probably parabola, each ball just have lower path. But actually any path will create fascinating animation.

now we know position of each ball at time t, its easy to create an animation.

one way to create animation is to know position of each object in any frame.

a higher level way to create animation is, know an object's begin and end position, and specify a rule to determine their intermediate positions.

if you know a better way, post it.

• Wolfram: Animation

• Xah Talk Show 2025-03-26 Ep635 Wolfram language, graphics for beginner, draw pedal curve
• Wolfram Language Tutorial
• Mathematica Packages for Plane Curves
• Emacs: Xah Wolfram Mode 📦

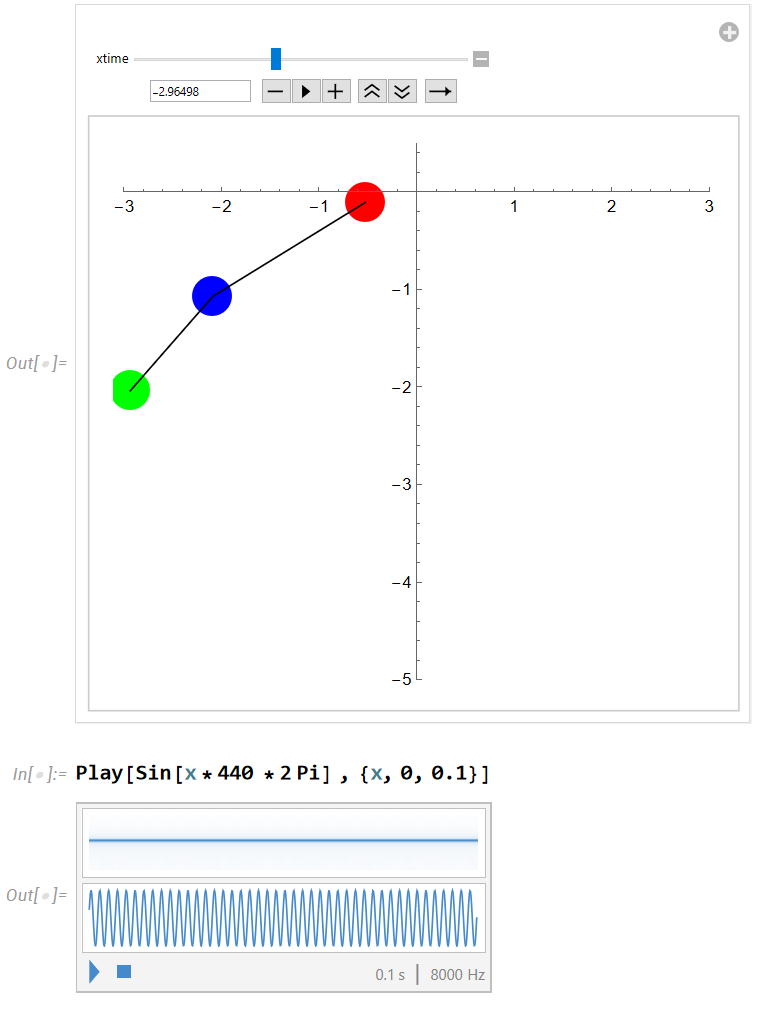
(* graphics of a disk *)
Graphics[Disk[{0,0},1] ,
Axes -> True ,
PlotRange -> {{-1,1} 30, {-1,1} 30}
];

(* HHHH------------------------------ *)

(* parabola *)
Plot[ -x^2  , {x, -9, 9}]

(* HHHH------------------------------ *)

(* all the balls are in sync, from beginning time param, to end of time param *)

xanimation =
  Graphics[{{Red, Disk[{xtime, -xtime^2}, 0.2]}, {Blue,
     Disk[{xtime*0.8, -(xtime*0.8)^2 - 1}, 0.2]}, {Green,
     Disk[{xtime*0.6, -(xtime*0.6)^2 - 2},
      0.2]}, {Line[{{xtime, -xtime^2}, {xtime*0.8, -(xtime*0.8)^2 -
         1}, {xtime*0.6, -(xtime*0.6)^2 - 2}}]}}, Axes -> True,
   PlotRange -> {{-1, 1}  4, {-4, 0.5}}];

Manipulate[Evaluate@xanimation, {xtime, -2, 2}]

(* HHHH------------------------------ *)

Play[Sin[x*440*2 *2  Pi] , {x, 0, 0.1}]

(* HHHH------------------------------ *)

Clear[xtimeMax, xmax, yMaxHeigh, ymax, ball1Pos, ball2Pos, ball3Pos, xanimation];
xtimeMax = 20;
xmax = 3;
yMaxHeigh = 5;
ymax := yMaxHeigh/xtimeMax^2;

ball1Pos := {Sin[xtime] xmax, -xtime^2 ymax};
ball2Pos := {Sin[xtime*0.6] xmax, -(xtime*0.6)^2 ymax - 2};
ball3Pos := {Sin[xtime*0.8] xmax, -(xtime*0.8)^2 ymax - 1};

xanimation :=
Graphics[
{{Red, Disk[ball1Pos, 0.2]},
 {Blue, Disk[ball2Pos, 0.2]},
 {Green, Disk[ball3Pos, 0.2]},
 Line[{ball1Pos, ball2Pos, ball3Pos}] },
Axes -> True,
PlotRange -> {{-1, 1} xmax, {-yMaxHeigh, 0.5}}];

Manipulate[ Evaluate@
{
xanimation,
If[ xtime > (xmax -0.2),
EmitSound@ Play[Sin[x*440*2 *2  Pi] , {x, 0, 0.05}],
Nothing ]
} ,
{xtime, -xtimeMax, xtimeMax}]