Xah Talk Show 2025-12-11 Ep723 Wolfram Language, Advent of Code 2025, Day 1, Problem 2, take 2

https://youtu.be/kqNXM-DJ3rY

https://adventofcode.com/2025/day/1

2025-12-11

Why Wolfram language QuotientRemainder[-10,3] return {-4, 2}, not {-3, 1}

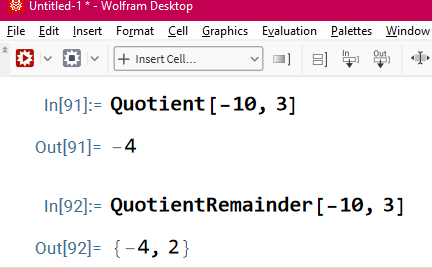
xah talk show ep723 Wolfram language QuotientRemainder 2e893

QuotientRemainder[10,3]
(* {3, 1} *)

(* why does this not return {-3, 1} *)
QuotientRemainder[-10,3]
{-4, 2}

Quotient[-10,3]
(* -4 *)

because, it is to be consistent with Quotient function, and the Quotient function doc says:

Quotient[m,n] gives the greatest integer no larger than m/n.

in other words, it rounds using Floor.

Quotient

2025-12-11

why quotient(10,-3) return -4, not -3

when doing quotient(10,-3) why does it return -4, not -3.
what is the math convention, for quotient(-10,3) to return -3 or -4
https://x.com/i/grok/share/CQV0w07CHxzYTpSs37s2PfHZk

grok gave several incorrect answer.

1. there is is no math.quotient in python.
2. grok ai saying that JavaScript quotient function truncates towards 0, is incorrect. because in JavaScript, there is no integer quotient function.
3. the reason it says the convention is remainder to be non-negative, but quotient(-10,3) return -3 is also valid, because -3*-3 = 9+1.

print(10 // 3)
# 3

print(-10 // 3)
# -4

Clear[xOperation]

xOperation::usage="xOperation[currentNumber, rotateN]
returns a list
{c,d}
c is the number of times it passed 0.
d is the new index number.";

(* this function is incorect.
when, currentNumber is 0 , and the result index number is also 0.
in this case, the returned value First Part sould minus 1.
 *)

xOperation[currentNumber_, rotateN_] :=
QuotientRemainder[(currentNumber + rotateN) , 100]

xOperation[0,0]
(* {0, 0} *)

xOperation[0,5]
(* {0, 5} *)

xOperation[0,100]
(* {1, 0} *)

xOperation[0,101]
(* {1, 1} *)

xOperation[0,-100]
(* {-1, 0} *)

xOperation[5,0]
(* {0, 5} *)

xOperation[5,-4]
(* {0, 1} *)

xOperation[5,-5]
(* {0, 0} *)

xOperation[5,-6]
(* {-1, 99} *)

xOperation[5,-99]
(* {-1, 6} *)

xOperation[5,-100]
(* {-1, 5} *)

xOperation[5,-600]
(* {-6, 5} *)

xOperation[5,5]
(* {0, 10} *)

xOperation[5, 600]
(* {6, 5} *)