Xah Talk Show 2026-01-24 Ep749 Wolfram Language, Advent of Code 2025, Day 8

2026-01-24

https://youtu.be/r3rvPj2_HEg

2026-01-25

xtodo

Video Summary (Generated by AI, Edited by Human.)

The video, titled "Xah Ep749 Wolfram Language, Advent of Code 2025, Day 8," focuses on the speaker's attempt to solve an Advent of Code 2025 problem, specifically Day 8, using Wolfram Language.

Here's a breakdown of the key topics:

Introduction and Setup (0:02-1:51): The speaker greets the audience and introduces the topic, showing his keyboard setup (Ultimate Hacking Keyboard, trackball, Logitech) and mentioning he has reviews for them. He then switches to his screen to begin the Advent of Code problem. He also highlights his frustration with Windows' auto-snap-window feature.
Advent of Code Website Criticism (2:01-2:28): The speaker expresses his dislike for the Advent of Code website's design, noting its fixed layout design. on larger screens and the need for horizontal scrolling.
Emacs and Word Wrap Tip (2:32-4:41): He switches to Emacs to read the problem description, demonstrating how to use the word wrap feature (4:31-4:41) for better readability, offering a tip for Emacs users.
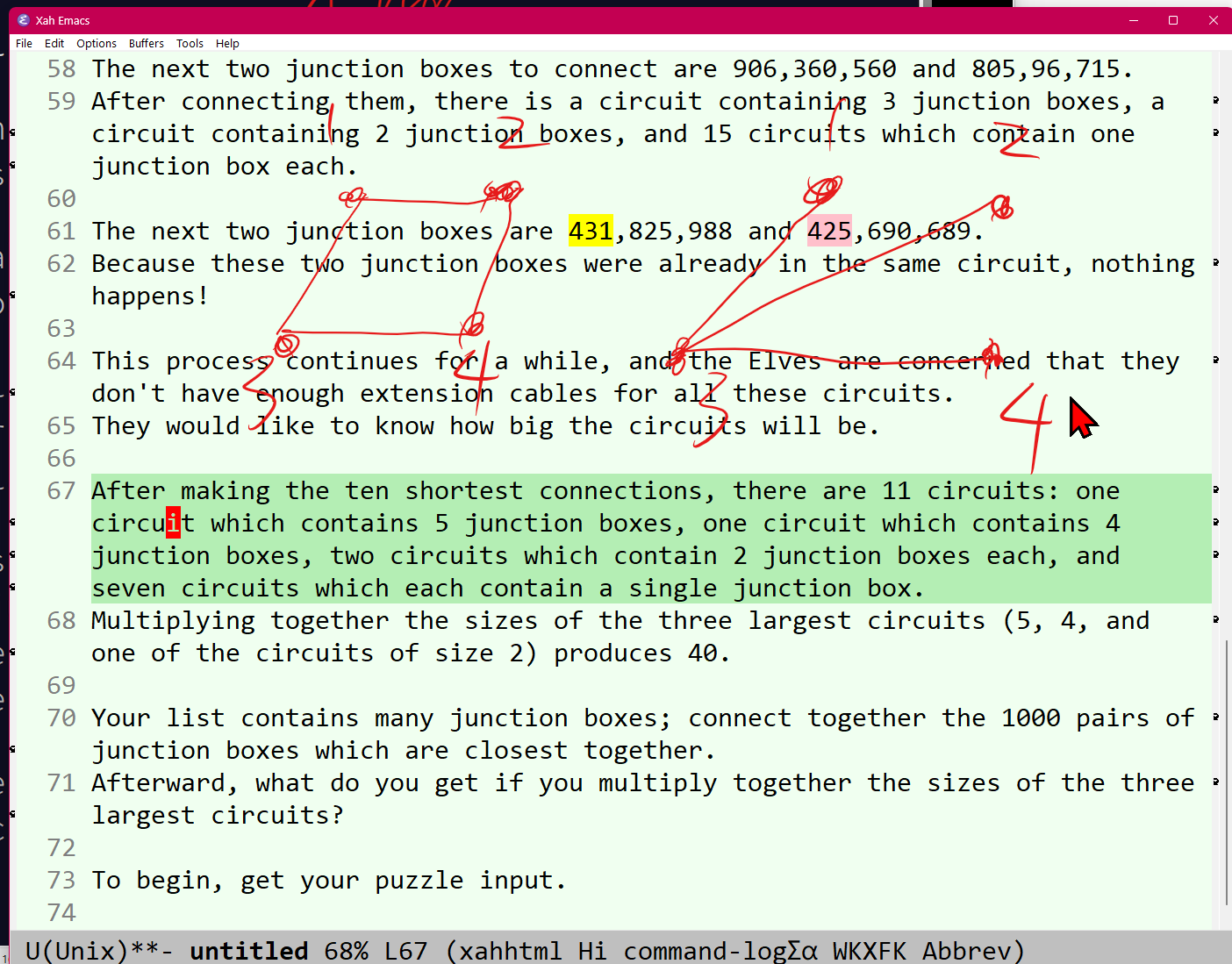
Problem Description and Initial Confusion (4:47-13:19): The speaker begins reading the lengthy and, in his opinion, "incomprehensible" and "irrelevant" story behind the Advent of Code problem. The problem involves "junction boxes" in 3D space, which need to be connected by "strings of lights" based on their "straight line distance." He initially struggles to understand the rules of connection and circuit formation.
Combinatorial Analysis of Points (13:53-20:00): The speaker delves into the mathematical aspect of the problem, discussing how many possible pairings of points (junction boxes) exist. He calculates that for 20 points, there are 190 possible distances to measure, which he considers "not too bad" for brute force. He then estimates that for his personal input of 1,000 points, there would be approximately 500,000 pairings (20:10-20:30).
Audience Interaction and Digression (20:30-22:10): He greets viewers and briefly digresses into a discussion about the origins of some audience members (Scandinavia and India).
Continued Problem Interpretation (22:10-48:19): The speaker continues to grapple with the problem's mechanics, particularly the concept of "circuits" and how connections affect them.
Problem Analysis and Plan (48:20-56:00): The speaker finally articulates a clear understanding of the problem's two main parts:
Finding the top 1,000 shortest distances among all points.
Connecting these points based on these distances, forming "disjoint graphs" (or circuits as the problem defines them), and then multiplying the sizes of the three largest circuits. He considers the problem "not easy" and plans to solve it the next day.
Wolfram Language and Graph Theory (56:00-1:01:28): He briefly explores Wolfram Language's capabilities for graph theory, suggesting that built-in functions might simplify the solution. He then focuses on the distance formula for 3D coordinates and considers the feasibility of processing 500,000 distance calculations and sorting them, also musing on browser limitations when dealing with large arrays.

Emacs: Xah Fly Keys 📦

2026-01-24

xtodo

problem analysis

first, find the top 1k shortest distances among the points. Rank them (shortest come first.)

for each, start from the shortest, connet the points.
do this for all the 1k distances you found.
the result, is a bunch of disjoint graphs (or, all joined).

problem is, pick the 3 largest disjoint graphs, multiply their sizes.

(*
the distance formula between
{a,b,c} and
{x,y,z}
is
 *)

Sqrt @ Total @ (({a,b,c}- {x,y,z})^2)

(* Sqrt[(a - x)^2 + (b - y)^2 + (c - z)^2] *)

this first part, about finding list of shortest distances, is a classic computational geometry problem.

given n nodes, how many possible edges are there
https://x.com/i/grok/share/d701fefdd4e9420e8db26d6a896f5a07

would browser crash if i have 500k items in a array
https://x.com/i/grok/share/a7117bfdb2534b31a58c538713429aab

given n points in 2d space, what's a good algorithm to find the top ten shortest distances between any 2 points.
https://x.com/i/grok/share/aa796dcac29c44799f835f5abb2c2184