Xah Talk Show 2025-04-08 Ep640 Wolfram Language, Coding Graphics Function Negative Pedal

• https://youtu.be/xQW5xpu9zFA

• Parabola
• Pedal Curve
• Wolfram Language Tutorial
• Mathematica Packages for Plane Curves
• Emacs: Xah Wolfram Mode 📦

• clean up the code of negative pedal
• Xah Talk Show 2025-03-26 Ep635 Wolfram language, graphics for beginner, draw pedal curve

Clear[NegativePedalPlot]

NegativePedalPlot::usage =
"NegativePedalPlot[{xf,yf}, {min, max, step}, {x0, y0}]
Draws the negative pedal lines of the parametric curve {xf,yf} at points from min to max with step
xf and yf must be pure functions with head Function.
Example:
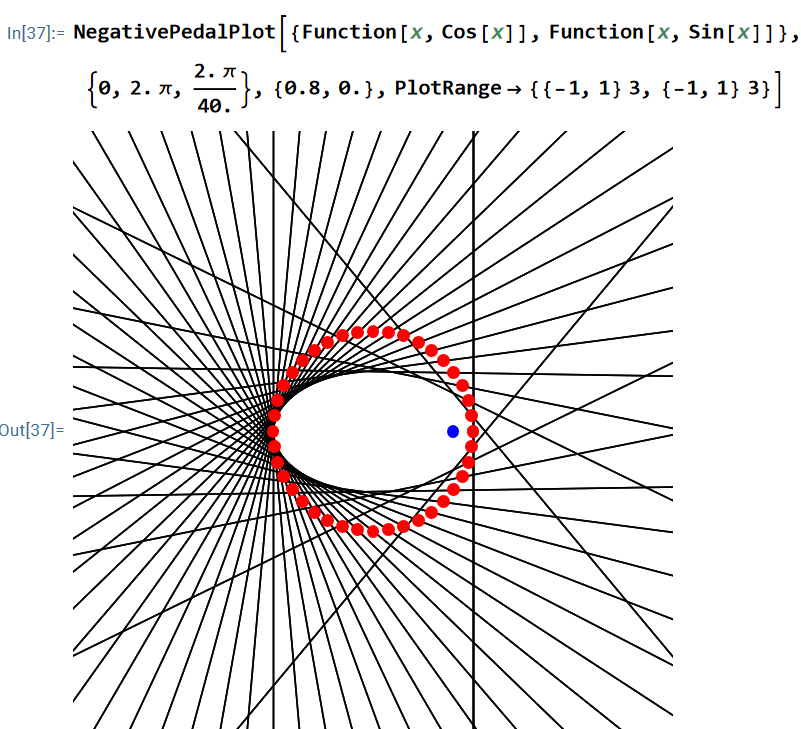
NegativePedalPlot[ {Function[x, Cos[x]], Function[x, Sin[x]]}, {0, 2.*Pi, (2.*Pi)/40.}, {0.8, 0.}, PlotRange -> {{-1, 1}*3, {-1, 1}*3}]";

NegativePedalPlot[{xf_Function, yf_Function}, {tmin_, tmax_, dt_}, {a_, b_}, opts___Rule] :=
 Module[{curvePoints, curvePointsGP, pedalPointGP, linesToCurveGP,
   negativePedalLinesGP},
  curvePoints =
   Map[Function[x, {xf[x], yf[x]}], Range[tmin, tmax, dt]];
  curvePointsGP =
   Map[Function[{Red, PointSize[.02], Point[#]}], curvePoints];
  pedalPointGP = {Blue, PointSize[.02], Point[{a, b}]};
  linesToCurveGP = Map[Function[Line[{{a, b}, #}]], curvePoints];
  negativePedalLinesGP =
   Map[Function[
     Line[{100  Reverse[
          Normalize[# - {a, b}] {1, -1}] + #, -100  Reverse[
          Normalize[# - {a, b}] {1, -1}] + #}]], curvePoints];
  Graphics[{negativePedalLinesGP, curvePointsGP, pedalPointGP}, opts]]

(* HHHH------------------------------ *)

NegativePedalPlot[
{ Function[{x}, x], Function[{x}, x^2/4 ] },
{-7, 7, .25},
{0, 1},
Axes -> True, AspectRatio -> Automatic,
PlotRange -> {{-7, 7}, {-1, 18}}]