Pedal Curve
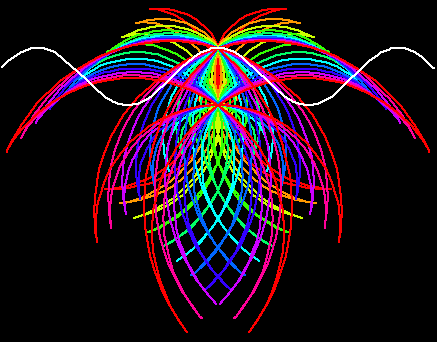
History
From Robert Yates:
The idea of positive and negative pedal curves occurred first to Colin Maclaurin in 1718; the name “pedal” is due to Terquem. The theory of Caustic Curves includes Pedals in an important role: the orthotomic is an enlargement of the pedal of the reflecting curve with respect to the point source of light (Quetelet, 1822). (See Caustics.) The notion may be enlarged upon to include loci formed by dropping perpendiculars upon a line making a constant angle with the tangent, namely: pedals formed upon the normals to a curve.
Description
Pedal and negative pedal
- Pedal and negative pedal are methods of deriving a new curve based on a given curve and a point.
- Pedal and negative pedal are inverse concepts.
- Negative pedal of a curve C can be defined as a curve C' such that the pedal of C is C'.
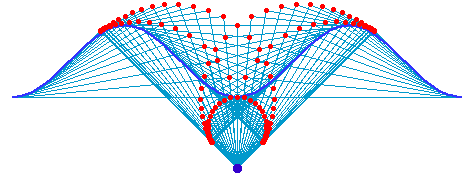
Positive Pedal
Step by step description for positive pedal:
- Given a curve and a fixed point O.
- Draw a tangent at any point P on the curve.
- Mark a point Q on this tangent so that line PQ and line OQ are perpendicular.
- Repeat step (2) and (3) for every point P on the curve. The locus of Q is the pedal of the given curve with respect to point O.
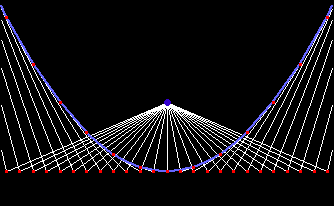
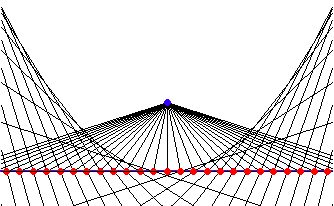
Negative Pedal
Step by step description for negative pedal:
- Give a curve and a fixed point O.
- Draw a line from O to any point P on the curve.
- Draw a line perpendicular to line OP and passing P.
- Repeat step (2) and (3) for every point P on the curve. The envelope of lines is the negative pedal of the given curve with respect to point O.
Formula
The pedal of a parametric curve {xf[t],yf[t]} with respect to point {a,b} is:
{(xf'[t]^2 a + yf'[t]^2 xf[t] + xf'[t] yf'[t] (b - yf[t]))/(xf'[t]^2 + yf'[t]^2), (yf'[t]^2 b + xf'[t]^2 yf[t] + xf'[t] yf'[t] (a - xf[t]))/(xf'[t]^2 + yf'[t]^2)}
Properties
Curve relations by pedal
| Base Curve | Pedal Point | Pedal Curve |
|---|---|---|
| line | any point | point |
| circle | any point | limacon of Pascal |
| circle | on circumference | cardioid |
| parabola | on directrix | strophoid |
| parabola | center of directrix | right strophoid |
| parabola | reflection of focus by directrix | trisectrix of Maclaurin |
| parabola | vertex | cissoid of Diocles |
| parabola | focus | line |
| ellipse, hyperbola | focus | circle |
| Tschirnhausen's cubic | focus of pedal? | parabola |
| cissoid of Diocles | focus | cardioid |
| cardioid | cusp | Cayley's Sextic |
| deltoid | cusp | simple folium |
| deltoid | vertex | double folium |
| deltoid | center | trifolium |
| deltoid | on the curve | unsymmetric double folium |
| epicycloid | center | rose |
| hypocycloid | center | rose |
| astroid | center | quadrifolium |
| sinusoidal spiral | pole | sinusoidal spiral |
| equiangular spiral | pole | equiangular spiral |
| involute of a circle | center of circle | Archimedean spiral |