Xah Talk Show 2025-12-04 Ep718 Wolfram Language, Custom Function, 2d Graphics to SVG. Part 2
Video Summary (Generated by AI, Edited by Human.)
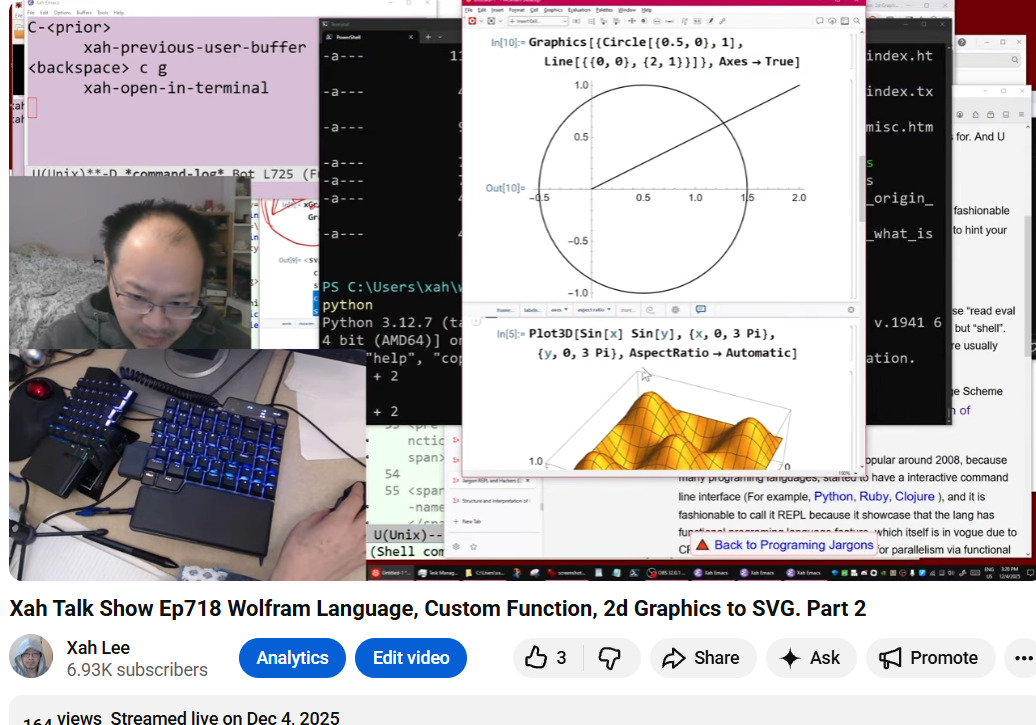
This video is the second part of a series focusing on writing a custom Wolfram Language function to convert Wolfram Language graphics to SVG.
Here's a summary of what's covered:
- The creator demonstrates how to define and use Wolfram Language functions, specifically showing how to create graphics using primitives like Circle and Line (4:29, 56:00).
- The core of the video involves enhancing a previously written function called graphicsToSVGString to convert both Circle and Line graphic primitives into their corresponding SVG string representations (15:57, 56:00).
- A significant portion of the video discusses Wolfram Language's computational model, emphasizing its basis in pattern matching and term rewriting systems (26:59). This is contrasted with other programming language models.
- The creator then modifies the function to save the generated SVG string directly to a file, demonstrating the WriteString function (1:00:37).
- Finally, the video touches upon the challenges of converting Wolfram Language coordinates to SVG coordinates, including issues with origin centering, y-axis reversal, and the need for coordinate rescaling using SVG's viewBox (1:13:25).
The video discusses different "centers" of a triangle, which are specific points within or related to a triangle. The speaker mentions the following:
- Circumcircle/Circumcenter (23:29): A circle that passes through all three vertices of a triangle. The center of this circle is the circumcenter.
- Inscribed Circle/Incenter (24:27): A circle of maximum size that fits inside a triangle, touching all three sides. The center of this circle is the incenter. The incenter is also described as the point where the three interior angle bisectors intersect (33:51).
- Other Centers: The video briefly touches on other centers like the centroid (34:42) and orthocenter (34:49). These are mentioned as part of a broader concept of "so-called centers" in geometry.
The video discusses the concept and history of notebooks, particularly in the context of the Wolfram Language.
- Origin: The speaker states that Wolfram Language (Mathematica) invented the notebook interface in 1989, making it the first of its kind (32:55).
- Jupyter Notebook: Jupyter Notebook is mentioned as a popular example that copied the Wolfram Language's notebook idea (33:01, 37:47).
- Advantages over Command Line/REPL: The speaker emphasizes that the notebook interface is superior to a command-line interface (CLI) or a "REPL" (Read-Eval-Print Loop) (47:09). Notebooks allow you to jump to and modify any part of the code at any time, unlike CLIs which are linear and force you into sequential input/output (47:09-47:45).
- Features: Notebooks can include features like headers, sections, bold/italic formatting, and automatic formatting/indentation of code (38:19, 53:02).
- https://youtu.be/erdFRplgF24?t=1618
- Wolfram Language's computational model, emphasizing its basis in pattern matching and term rewriting systems (26:59).
- This is contrasted with other programming language models, e.g. c, cpp, golang, python, lisp.
- Wolfram Language for Programers
- Wolfram: Download Wolfram Engine
- Emacs: Xah Wolfram Mode 📦
- Emacs: Xah Fly Keys 📦
- Jargon REPL and Hackers (2013)
- Structure and Interpretation of Computer Programs (SICP), Scheme LISP, JavaScript
- Command Line Interface (REPL) vs Notebook Interface
- Emacs: Evaluate Elisp Code
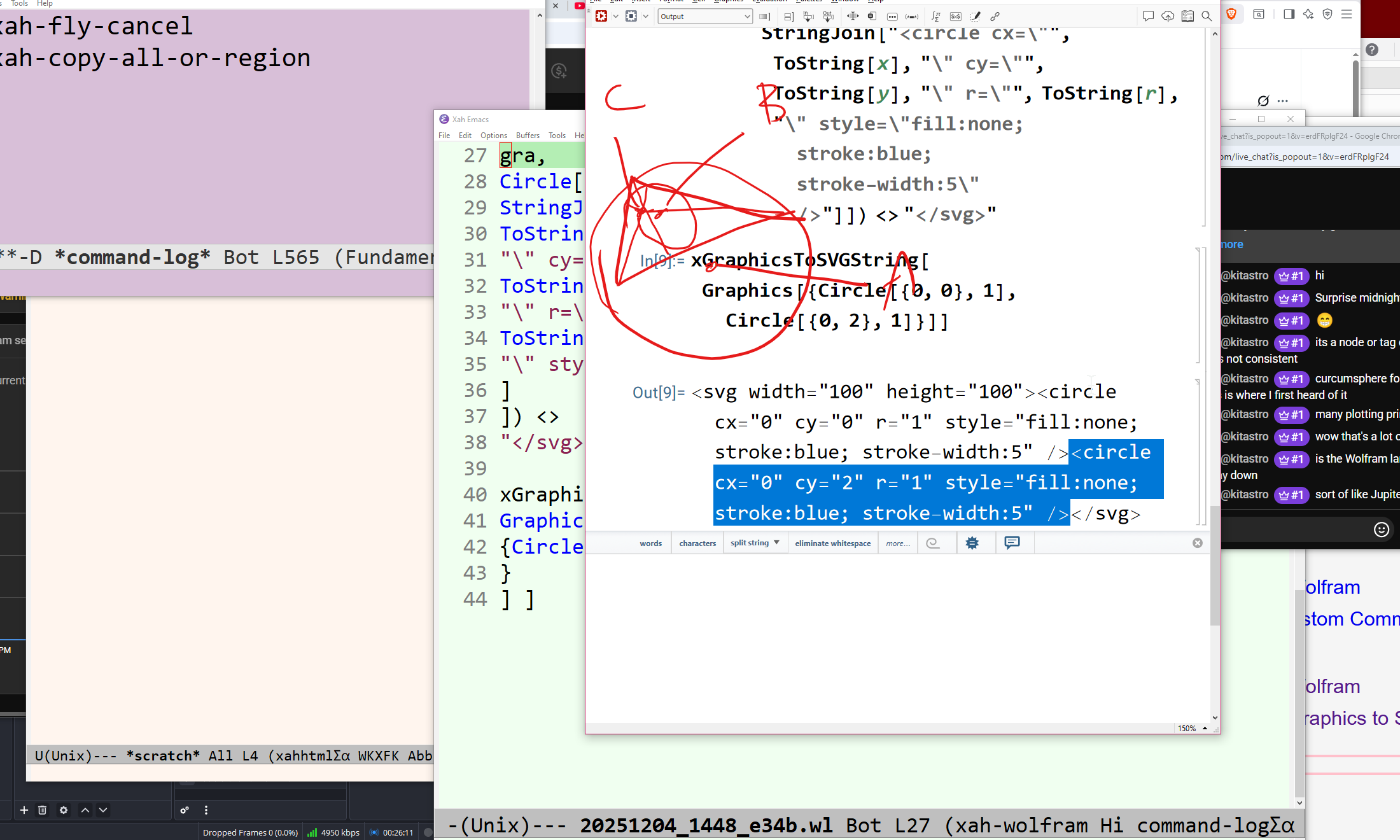
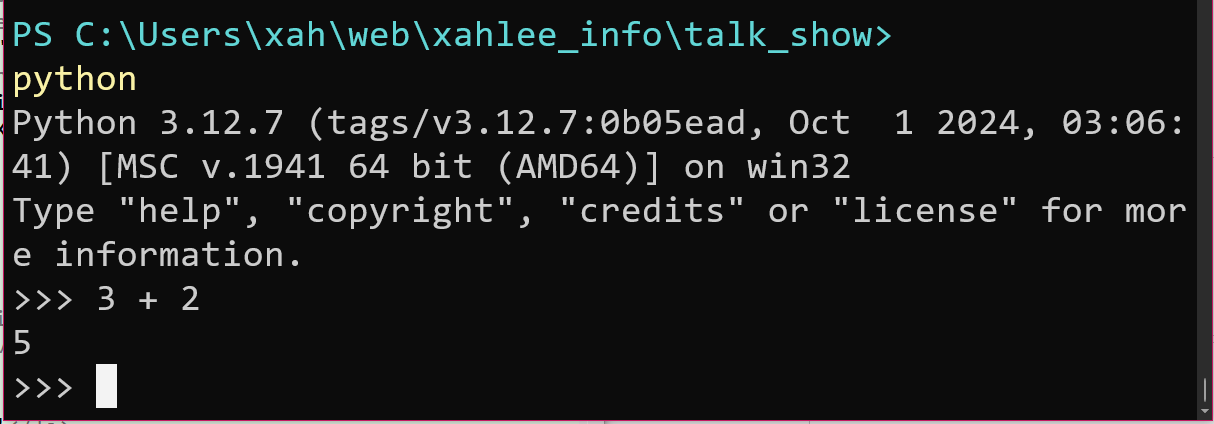
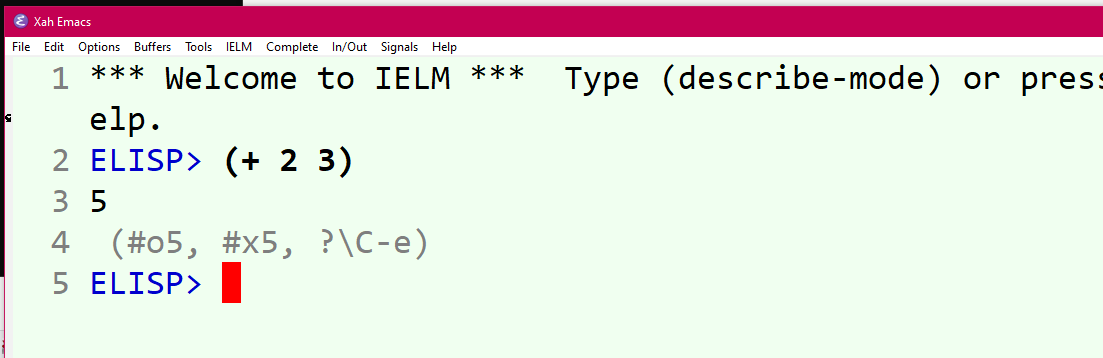
Graphics[Circle[{0, 0}, 1]] Graphics[Circle[{0, 0}, 1], Axes -> True] Graphics[ { Circle[{0, 0}, 1], Line[{{0,0},{2,1}}] } , Axes -> True]
StringJoin["some" , "thing"] (* something *) "some" <> "thing" (* something *)
(* 2 days ago, we wrote this function that convert circle to svg. today, we gonna modify the function, so it does lines too. and, we gonna make it actually export to a file. *) Clear[xGraphicsToSVGString] xGraphicsToSVGString::usage = " xGraphicsToSVGString[xGraphics] return a string that is svg representation of xGraphics. xGraphics is any expression with head Graphics. "; xGraphicsToSVGString[ Graphics[gra_] ] := "<svg width=\"100\" height=\"100\">" <> (StringJoin @ ReplaceAll[ gra, { Circle[ {x_, y_}, r_] :> StringJoin["<circle cx=\"", ToString[x], "\" cy=\"", ToString[y], "\" r=\"", ToString[r], "\" style=\"fill:none; stroke:blue; stroke-width:5\" />" ], (* <line x1="0" y1="0" x2="50" y2="10" style="stroke:black" /> *) Line[ {{a_, b_}, {c_, d_}}] :> StringJoin["<line x1=\"", ToString[a], "\" y1=\"", ToString[b], "\" x2=\"", ToString[c], "\" y2=\"", ToString[d], "\" style=\"stroke:black; stroke-width:5\" />" ] } ]) <> "</svg>" Clear[xGraphicsToSVGFile] xGraphicsToSVGFile::usage = " xGraphicsToSVGFile[xGraphics, xFilepath] Export xGraphics to SVG string and save it at xFilepath. xGraphics is any expression with head Graphics. "; xGraphicsToSVGFile[ xexpr_, xfilepath_ ] := ( WriteString[ xfilepath, xGraphicsToSVGString[xexpr]]; Close[ xfilepath ] ) (* xGraphicsToSVGFile[ xexpr_, xfilepath_ ] := *) (* CompoundExpression[WriteString[ xfilepath, xGraphicsToSVGString[xexpr]] *) (* , *) (* Close[ xfilepath ] *) (* ] *) (* s------------------------------ *) xGraphicsToSVGFile[ Graphics[ { Circle[{0, 0}, 1] , Circle[{0, 2}, 1], Line[{{0, 0}, {2, 1}}] } ], "my-fantastic-function.svg" ] (* success. next to do. need to center the origin. need to reverse the y axes. need to rescale the coordinate, i.e. svg viewBox. *)