Illustrating Geometry with POV-Ray
POV-Ray has very good application in geometry learning, but this aspect is almost never utilized.
In this page, i give some examples showing how POV-Ray, or any other 3D Graphics engine, can be put to good use in understanding math theorems, understanding perspective in art, and learning physics of optics.
Perspective in Visual Art
In visual art, one important concept is perspectivity. The concept and correct understanding came to artisan only after 1400s, which made a major change in the art world, where paintings transformed from mainly juxtaposition of imageries to realism.
The essence of perspective is a simple theorem in projective geometry: two parallel lines, when projected onto a plane, their projected image on the plane will intersect in a point, unless the parallel lines are parallel to the plane.
This simple fact can be easily illustrated with POV-Ray.
Perspective is a basic lesson for students of drawing. In drawing textbooks, they talk about “one-point perspectivity”, “two-point perspectivity”, “three-point perspectivity”. And, what happens if the two “vanishing points” are moved nearer or further apart.
All these principles can easily and truthfully be illustrated with POV-Ray.
Projective Geometry
Another example is its use in illustrating and studying projective geometry.
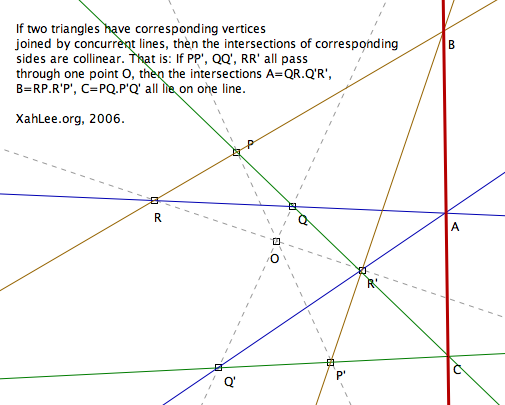
There is a three dimensional proof of the theorem by von Staudt, which involves projections of several triangles in 3D space. However, it is rather difficult to picture this in the mind.
With POV-Ray (or any graphics engine), one can easily picture this, either for the purpose of teaching (as illustration in textbooks), or to convince oneself.
Projections
The theories or concept of projection is a subject with wide-ranging applications, used in for example map-making (cartography), in studying art photography or filming (choices of lens, panorama), and not to mention in math for example the so-called Riemann sphere, or the projection of a highly decorated semi-regular polyhedron onto a sphere.
To illustrate these, POV-Ray is exceedingly handy. For example, to understand fish-eye lens or lenses with some other properties, one can use the graphic engine's built-in feature of various projections, as to render a scene with the lens. With this, one can experiment and understand the effects of with various lens/projections without actually having to have a camera with such a lens, some of which are physically impossible to build.
The stereographic projection in mathematics, can be illustrated by casting shadows of images on a glass-sphere, from the tip of the sphere.
Suppose the earth is a glass sphere, with its continents slightly tinted in color. Then, one can place this glass-sphere on a plane, and have a light source at the north pole, shining thru the sphere. The rendered result, will be a beautiful image showing the stereographic projection. Similarly, one can use grids or other tilling on the glass sphere, as to generate various other beautiful images on the plane. Also, instead of using a plane, one can put the glass sphere inside a glass tube. The result will be a cylindrical projection.
Solid Geometry and the Imagination
3-Cuts to a Donut
There is a math puzzle that goes like this: What is the maximal number of pieces you can get, by 3 planar cuts thru a donut?
This puzzle i read in Martin Gardner's Scientific America collection in the early 1990s. It is a wonderful puzzle. Its wonderment lies in the fact that it is torturous to picture this in the mind's eye. Nor is this easily resolved by trying to draw it on paper.
The answer, or the pleasure of trying to find the answer, can be easily illustrated with POV-Ray, which otherwise is difficult unless you are a artist who has studied technical drawing for years.
Conic Sections
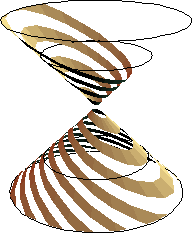

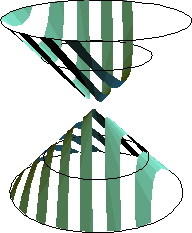
As we know, conic sections is the intersection of a cone and a plane. There are great many theorems of solid geometry involving conic sections.
For example, the very definition by slicing a cone with a plane to form ellipses, hyperbolas, and parabola. POV-Ray can be put to use in illustrating these.
The theorem of “Dandelin Sphere” states that the maximal sphere inside the cone will touch the cutting plane in the conic section's focus. This in another good application of POV-Ray.
A paradox about ellipses is that, since ellipse is symmetrical, how can a slice of a cone become a ellipse, and not some egg-shaped oval? Also, it is a theorem that the intersection of a cylinder and a plane is also a conic section. This doesn't seems intuitive.
POV-Ray can be employed to show these paradoxes. For example, by using its constructive solid geometry feature to actually slice a cone. Then, view the cutting plane face-on. The viewer should see a symmetrical figure. Further, one can also slice a cylinder, then match the sliced cylinder and the sliced cone such that their wound match perfectly, thus visual and computationally “proving” the theorem.
For some detail about conic sections, see: Conic section.
Ortho-Sculpture
There is a somewhat popular puzzle for geometric mental exercise: Try to imagine the exact shape of a object, that is made by the intersection of 3 orthogonal cylinders.
Such a figure will look like a circle if viewed from the sides, and will actually have a regular hexagon outline if viewed in some perspective. (Try to think about this for 10 minutes. The answer is on this page: POV-Ray: Constructive Solid Geometry.)

Note the famous book Godel, Escher, Bach. Its cover is a object such that when viewed from 3 orthogonal angles, it has the outline of the letters G E B respectively. Douglas Hofstadter actually designed and carved it out of wood blocks.
We can imagine a recreational math problem of this this theme. Suppose you are given all the letters of the alphabet in a particular font. Now, you are going to project the outline of any of 3 letters orthogonally into the face of a cube. The question is, which combination of 3 letters will produce a sculpture that is in one connected piece?
To make this problem more mathematically sound, we can think of the letter's font designs are patterns formed on a 5 by 5 grid.
xxxxx xxxx xxxxx x x x x x xxxxx xxx x x x x x x x x xxxx xxxxx … etc. something like that.
Then we can start to form theorems about the conditions that such a ortho-sculpture will not be in one-piece.
Another way to make this interesting, is to ask, given a sphere, and if we were to cookie stamp it from 3 orthogonal direction, then the resulting sculpture will have 3 different outlines when looked from the 3 direction of stamp. Now, what is the maximum number of stamping such that the sphere will have completely different view points? In other words, is it possible to have a shape such that, when looked from 26 different directions, will show 26 different letters in the alphabet?
With POV-Ray's Constructive Solid Geometry feature, one can easily create such sculpture, simply by creating the 3 or more cookie-stamps and intersect them.
Math and Illustrations
- Algorithmic Mathematical Art
- Art of M C Escher
- Escher Chameleon Polyhedron
- What is Technical Drawing, Descriptive Geometry, Projective Geometry, Linear Algebra
- Outline Rendering of 3D Models
- Autostereogram
- Visual Illusions
- Projective Illusion
- What Is Perspective Drawing
- Illustrating Geometry with POV-Ray
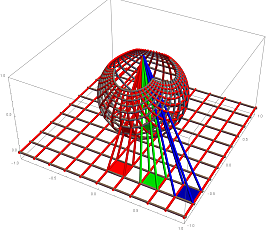 Stereographic Projection
Stereographic Projection