Lituus
History
The Lituus curve is studied by Roger Cotes in 1722 [Robert C Yates 1952].
The word lituus means a curved staff used by the augurs in quartering the heavens, or A kind of trumpet of a somewhat curved form and shrill note.
Description
Lituus is a spiral described by the polar equation r == 1/Sqrt[θ].
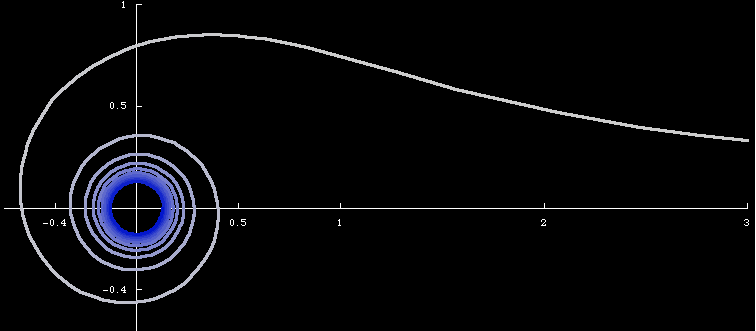
The curve is asymptotic to the positive x-axis, and the other end spiral in towards the pole. The above image is a plot from 0.1 to 20*Pi. As θ approachs infinity, the curve approaches the origin.
Formula
Polar equation: r == 1/Sqrt[θ].
Properties
It has the property that a circular sector produces the same area. That is, suppose P is a point on the curve, and X a point on the asymptote OP distance from the origin O. Suppose the area of the circular sector OPX is A. As P moves towards the center on the curve, the area remains the same.
inverse of parabolic spiral
The inverse of Lituus with respect to the center is the parabolic spiral.
misc
The lituus spiral is a recurring shape in art called Volute .
See Also
Archimedes' spiral, equiangular spiral, Math of Seashell Shapes.
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .