Cornu Spiral
History
These were considered by Euler at least as early as 1743 in a problem of his celebrated work on the calculus of variations: Methodus inveniendi lineas curvas maxime minimire proprietate gaudentes.
The spiral is also known as Euler Spiral, named after Leonhard Euler, or Cornu Spiral, after Marie Alfred Cornu .
Steven Schwartzman, in The Words of Mathematics Buy at amazon, suggests it derives from Greek kloth (“to twist by spinning”). He suggests that the curve resembles a spinning wheel, and clothoid might be an allusion to Greek goddess Clotho who spun a thread of destiny.
Description
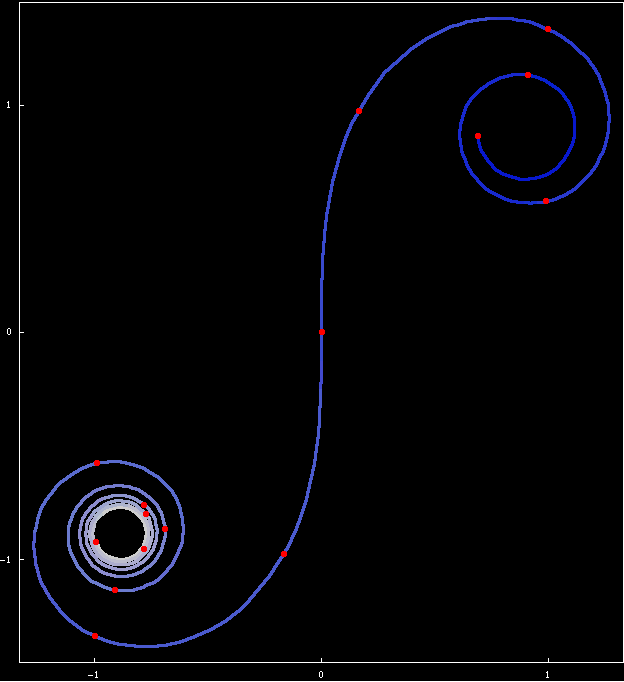
The clothoid is defined as the curve whose curvature is equal to its length. That is, the further the curve, the more curved it is. Such a curve is necessarily a spiral.
It is a curve invented in the era of differential geometry (in the 1700s), where mathematicians made precise the notion of curvature as the rate the curve changes directions (or, a measure of how “bent” a curve is at a given point on the curve). A theorem called the Fundamental theorem of curves is that a plane curve is essentially defined by its curvature.
Formula
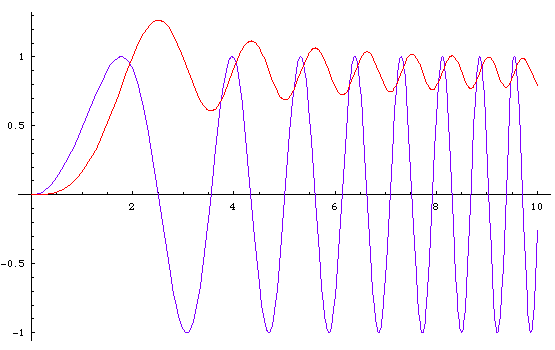
The clothoid is defined by this parametric formula:
{ Integrate[ Sin[(x^2)/2], {x,0,t}],Integrate[ Cos[(x^2)/2], {x,0,t}] }
Properties
Arclength and Curvature Equality
The function to compute the lenth of a curve {xf[t],yf[t]} from a to b is:
Integrate[ Sqrt[ xf'[t]^2 + yf'[t]^2] , {t,a,b} ]
Apply this to the clothoid parametric formula above, we obtain t. This means the parametric formula for clothid given above is such that the curve's arclength function is just t itself.
The function to compute the curvature of a curve {xf[t],yf[t]} at b is:
( -yf'[b] * xf''[b] + xf'[b]*yf''[b]) / (xf'[b]^2 + yf'[b]^2)^(3/2)
Apply this to the clothoid parametric formula above, we obtain b. Since the arclength is also t, this means that the clothoid is the curve whose curvature varies identically in value with its length.
Generalization
We can generalized the Cornu Spiral by defining a curve such that, if its arclength is t, then its curvature is t^n. The formula for such a curve is this:
{ Integrate[ Sin[(x^(n+1))/(n+1)], {x,0,t}], Integrate[ Cos[(x^(n+1))/(n+1)], {x,0,t}] }
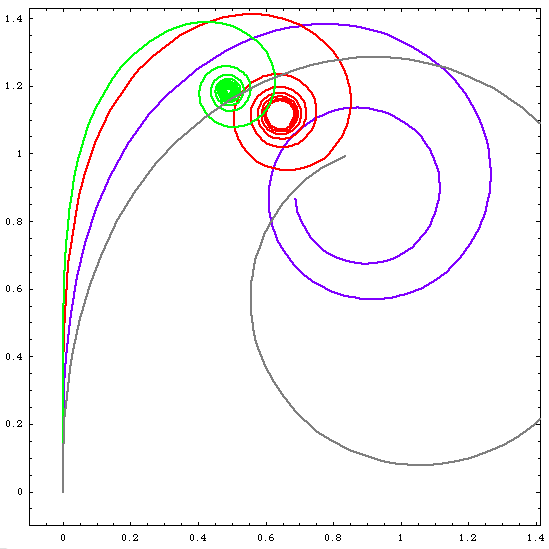
When n==0, the curve becomes a circle, with curvature t^0, as expected.
Related Web Sites
- Euler's Spiral, American Math Monthly Volume 25 (1918) Eulers_Spiral_American_Math_Monthly_Volume_25_1918.zip
Thanks to Greg Scott for etymology of clothoid.