Xah Math Blog Archive 2017-01
- Drawing fractal Droste images
- By Roy Wiggins.
- http://roy.red/fractal-droste-images-.html
this book i used back in 1992, and loved it.
get old edition, as newer edition of math textbook don't add much. are basically scams to get you buy new.
Why Are Textbook So Expensive?
i also like Abstract Analysis, Andrew Gleason
old article The Problems of Traditional Math Notation
hit hackernews https://news.ycombinator.com/item?id=15631151
2 great JavaScript for visualization
❰2017-11-03
❰2017-11-03
Automatic differentiation and differentiation without limits
from ~2017-10-17
https://plus.google.com/+XahLee/posts/hzPVxNEWbe1
comment at
https://plus.google.com/+XahLee/posts/49vT1MXY3Fn
Spivak's Calculus on Manifolds, why is Wikipedia linking to stolen pdf?
is Spivak's Calculus on Manifolds in public domain now? why's Wikipedia linking to pdf?
3dxm, worst math software, but great for visualization of manifold
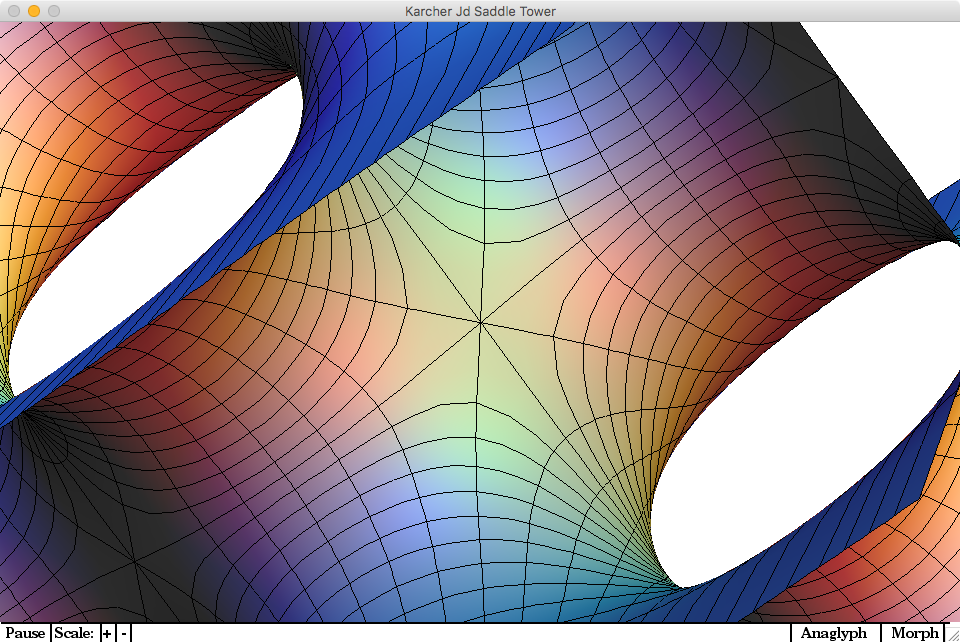
3dxm (aka 3d explore math), by my professor friends Richard Palais and Karcher Hermann, the worst software possible in the universe.
painful to use beyond comprehension
however, it is one of the best for visualizing manifold.
to see what the software can do, see:
- http://virtualmathmuseum.org/Surface/gallery_m.html
- http://virtualmathmuseum.org/Surface/gallery_o.html
you can download 3dxm at http://3d-xplormath.org/index.html
Riemannian Geometry and Mathematical Physics
Got a gift from John Baez:
GAUGE FIELDS, KNOTS AND GRAVITY by John Baez, Javier P Muniain, 1994.
excellent book. the book is really about the math of physics. More specifically, Riemannian Geometry.
the book is fast easy reading!
i think i start right at chapter 4 on differential forms.
then resolve the mysteries of stoke's theorem, exterior differential forms, cohomology, lie group, then,
in part 2 will be lots goodies for me. bundles and connection, homology. ... chern classes in chapter 4, ... and more differential geometry goodies in Part 3.
differential geometer Richard S Palais' Books and Papers http://vmm.math.uci.edu/PalaisPapers/
The Life and Mathematics of Shiing-Shen Chern
one of the greatest differential geometer of the century.
The Life and Mathematics of Shiing-Shen Chern
Just read this. Soul touching.
to read bio of Chern, is to also have a glimpse of modern history of China, thru the tumultuous times of war.
(watch great movie Farewell My Concubine )
and, i learned, a towering figure of differential geometry is Élie Cartan
math things i've learned.
equivalence problem. For example, triangle are defined by 3 real numbers, length of 2 of which is less than the other. So, that's the condition. It “generates” all possible triangles. And, any 2 triangle can be decided if they are equivalent (by isometry here), by first reducing the 3 numbers to certain canonical form (such as by scaling so that shortest side is 1), then simply compare the numbers.
For plane curves, it's determined by curvature function. It generates all plane curves. And to determine if 2 plane curves are equivalent by an isometry, you just express a given curve by the curvature function. Then you simply just compare 2 functions, literally.
for space curves, it's 2 functions: curvature and torsion.
for surfaces, it's the 2 fundamental forms.
the question of “equivalence problem”, is to formulate a way, so any 2 geometric object can be so compared, and unify the cases for curves and surfaces.
and Cartan began it Cartan's equivalence method
and today the method is “g structure”. G-structure on a manifold


see
https://plus.google.com/+johncbaez999/posts/DGYEUQ3WG4b
omg, how boring is topology?
you'd think you gonna see how coffee cup turns into a donut.
instead, you got a fiat “open set”. From there on, its set of sets, subset, empty set, union of set, intersection of set, complementary set, power set, super set, finer set, coarser set, and it's set all the way!
https://plus.google.com/+XahLee/posts/MqxVNtn572c
The Method of Fluxions by Issac Newton https://archive.org/stream/methodoffluxions00newt#page/n3/mode/2up
Hilbert's 16th problem. the relative positions of the branches of real algebraic curves of degree n. Hilbert's sixteenth problem
math notation idiocy
https://plus.google.com/+XahLee/posts/hzPVxNEWbe1
Comprehensive Introduction to Differential Geometry By Michael Splvak. Classic. Comprehensive Introduction Differential Geometry
that's 5 volumes heavy expensive book. and, is graduate level.
you wonder, why's such book named “introduction”. It's actually graduate text, at 5 thick heavy volumes. Mathematicians not specialized in differential geometry have lots to learn from it, i assume.
but, “introduction” implies, this 5 volumes book only touches the surface. But then, its got the word “comprehensive” in it?
so, the proper interpretation seems to be, that the topic of differential geometry really is deep, and tied with lots other advanced math. Therefore, even at 5 volumes, and being a comprehensive tome, is, still just a intro.
On several occasions, most prominently in Volume 2, Spivak “translates” the classical language that Gauss or Riemann would be familiar with to the abstract language that a modern differential geometer might use.
2017-10-08 Wikipedia Michael Spivak
that'd be interesting to read.
http://3d-xplormath.org/ for Mac
software for plotting math surfaces: Surfer
software for plotting math surfaces, especially algebraic surfaces. (Microsoft Windows, MacOS, Linux) https://imaginary.org/program/surfer
For some example of plots, see a friend Jean Constant's blog at https://jcdigitaljournal.wordpress.com/category/01-january-the-surfer-program/page/2/
Vladimir Voevodsky, Fields Medalist, Dies at 51
notation for recursion, what about notation for reduce?
been wanting a notation for recursion. Found it. In math, it's called iteration of a function, written as f^(°n). However, that doesn't cover reduce.
the term polytope is from mathematician Alicia Boole Stott. Alicia Boole Stott
understand the “expansion” operation on polyhedron
understand the “expansion” process on polyhedron. http://VirtualMathMuseum.org/Polyhedra/Icosahedron/index.html
Theory of Sets by N. Bourbaki Buy at amazon
- How real are real numbers?
- By Gregory Chaitin.
- https://arxiv.org/pdf/math/0411418.pdf
- (local copy How_real_are_real_numbers_By_Gregory_Chaitin_f76de.pdf)
gyroscopic precession

- https://youtu.be/eTjGTxSevHE
- Helicopter Physics Series - #4 They're Gyroscopes - Smarter Every Day 48
Learned about gyroscopic precession. Not intuitive. Don't know how the physics works out. But this video is amazing
Visualize Math with 3D Printing

Visualizing Mathematics with 3D Printing. one expensive book Buy at amazon
Heatmap of Trig Expressions. old. repost.
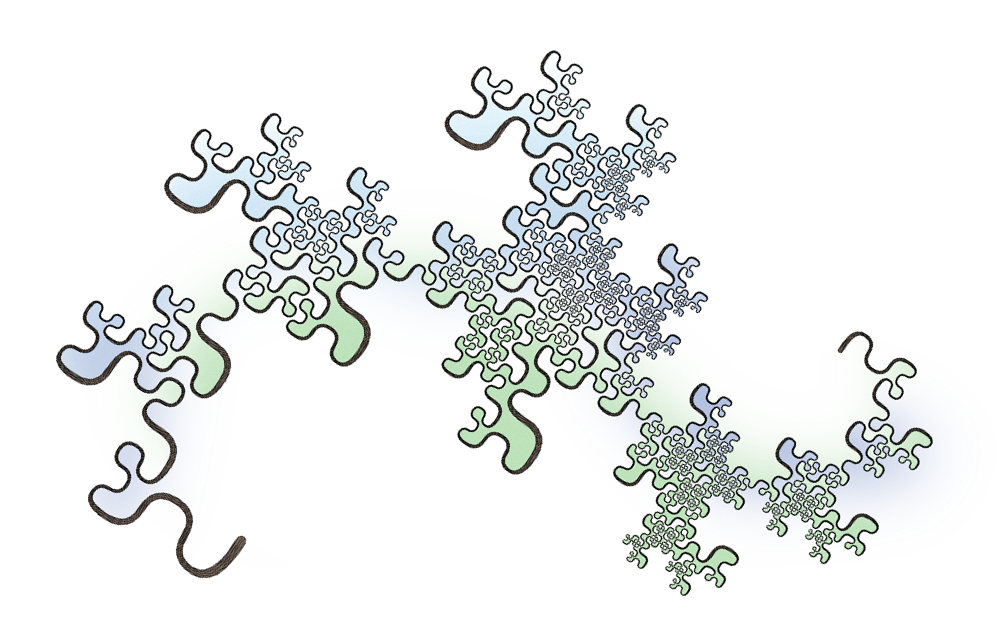
- All Plane-Filling Curves
- By Jeffrey Ventrella.
- http://fractalcurves.com/all_curves/
 Groups and Their Graphs by Israel Grossman and Wilhelm Magnus
Groups and Their Graphs by Israel Grossman and Wilhelm Magnus Visual Complex Analysis by Tristan Needham
Visual Complex Analysis by Tristan Needham Polyhedra Chocolate
Polyhedra Chocolate kolam pattern
kolam pattern