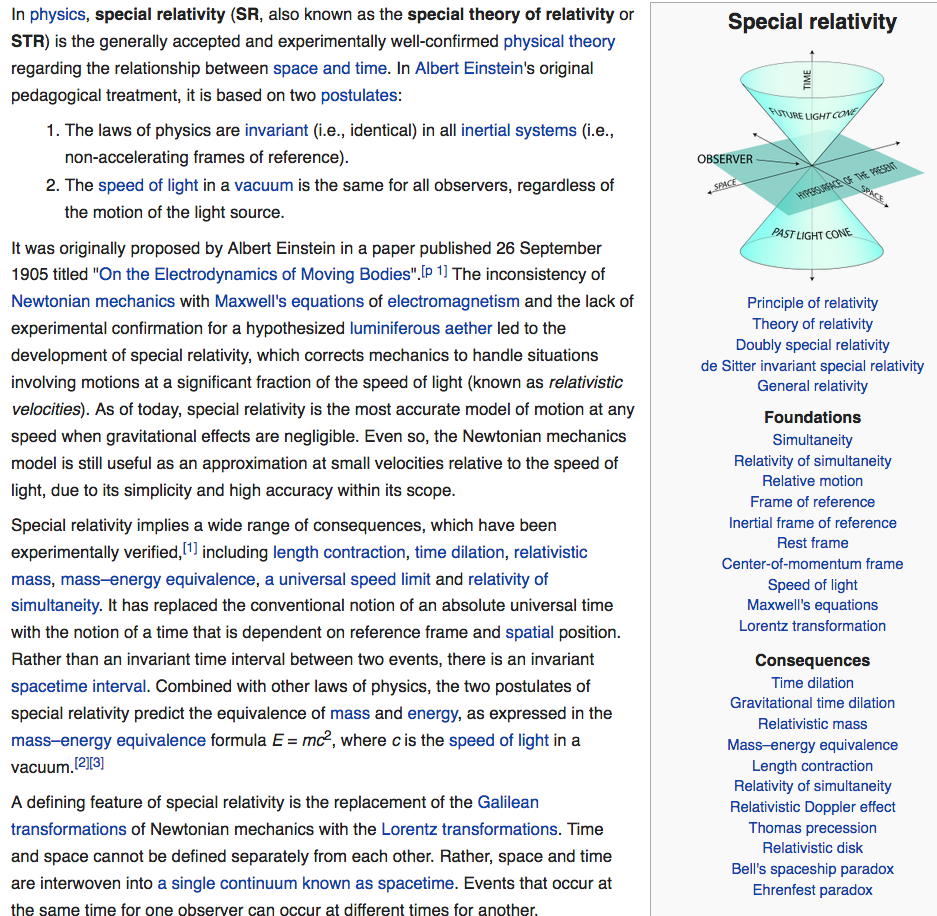
Xah Math Blog
Update Highlights
Local Constant Variable Chaining
- Wolfram language now support variable chaining in local constant block.
- was just complainting about this.

Cyclic List
- A new feature in Wolfram language is Cyclic.
- Basically this implement Lisp's cyclic list, sans the biddiddling voodoo.
- By simply using modular arithmetic on the index.
- This is the best approach.
Surface Curvature
find shortest path on a surface or region (geodesics)

- Math exercise.
- if you have a circle centered around origin with radius 1,
- and n circles it, touching it.
- what is the radius of the circles?
- you can ask ai bot.
- Geometric inversion.
- Most beautiful concept in math.
- It is, like, y = 1/x.
- Rearrange the equation, you get x y = 1.
- The large the x, the smaller the y.
- The x and y is like yin yang, they yield to each to reach harmony of 1.
- The x and y are called multiplicative inverse of each other.
- Similar is x + y = 0. where, if x is positive, y needs negative, and equal in size.
- this is called additive inverse.
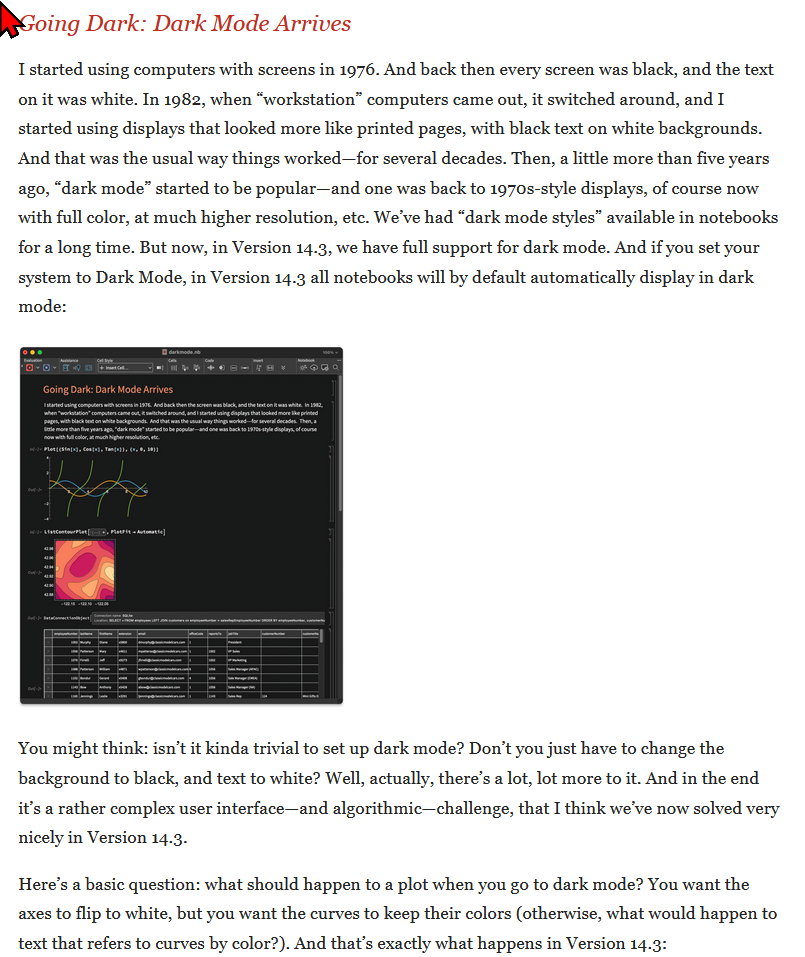
Stephen Wolfram's latest article
- New Features Everywhere: Launching Version 14.3 of Wolfram Language & Mathematica
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2025/08/new-features-everywhere-launching-version-14-3-of-wolfram-language-mathematica/
- Part of it discuss how involved it is to create a dark theme.
- This is true.
also, from Stephen Wolfram's blog. i just run the code. Amazing.

ArrayPlot3D[ Total[ CellularAutomaton[ Association[ "Dimension" -> 3, "GrowthCases" -> {1, 2, 3} ], {{{{1}}}, 0}, 15 ]] ]
- For Coders. Advanced Graphics Programing. Wolfram language and SVG.
- Wolfram language can export graphics into tens of formats, one of them is svg.
- However, it exports Circle by using Cubic bezier curves approximates.
- The problem of this is if you have lots circles, it increase file size by 10 times.
- This seems strange, because svg has a circle element.
- so am writing one to export 2d graphics to svg.
- but it is not trivial to do a good job.
- if all you have is circles and lines, easy.
- but you need to also export all coloring, thickness, etc styles.
- this becomes non-trivial.

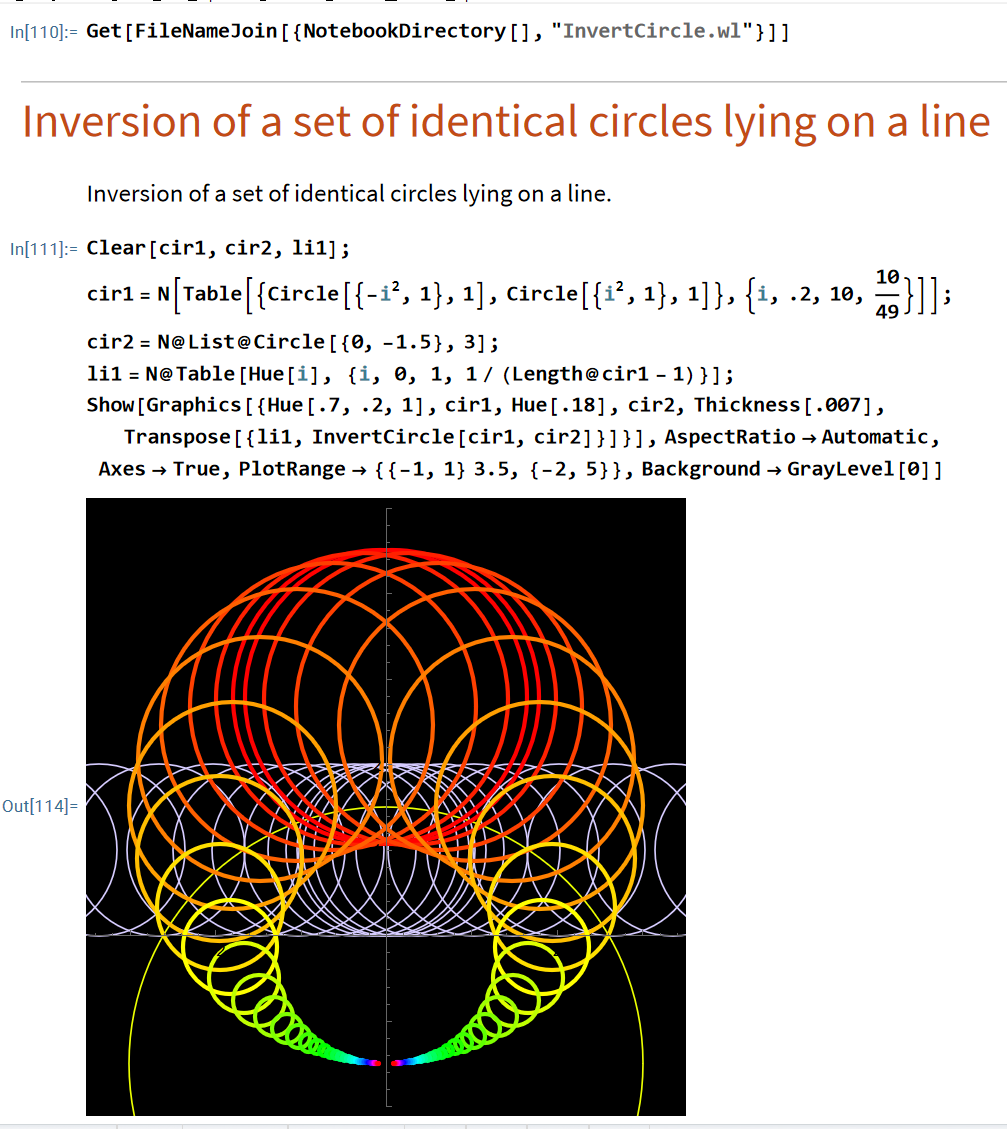
incoming
- xah invert circle package, Wolfram language
- Wolfram: Geometric Inversion Package 📦
Science and Art of Code Syntax
In Wolfram language, you have various options of notations. Here's some of them.
but notice, Wolfram doesn't like prefix notation or postfix notation. it converts prefix notation f @ x and postfix notation x // f to f[x]. Not sure i like that, because it increases nested brackets.

(* code from around 1998. The following is older code. The problem with using complex numbers to compute rotation is that when a value is Complex[0,0], it becomes just 0, and replacement back to List won't work. I.e. Won't match _Complex or just Complex->List *) InvertCircle[Circle[{c1_,c2_},s_],Line[{{a1_,a2_},{b1_,b2_}}]]:=Module[{rotV},rotV=(Complex[b1-a1,b2-a2])//(#/Abs@#&); (Complex[c1,c2]-Complex[a1,a2])//(#*Conjugate@rotV&)//(Conjugate@#&)//(#*rotV+Complex[a1,a2]&)//(Circle[#,s]/.x_Complex->{Re@x,Im@x}&)]
wow. wolfram language doc website has a new feature. now has side nav panel.
- why is mobius transformation also called Linear Fractional Transform
- https://x.com/i/grok/share/zNgiwv9ZCRMnOphS7rhi6k1rB

- My favorite concept in math is geometric inversion.
- Basically same as arithmetic inversion, the 1/x.
- Especially in complex numbers, the function 1/z.
- Inversion is a geometric transformation. The inversion of a point P with respect to a circle centered on O and radius r is a point Q such that OP*OQ==r^2.
- https://youtu.be/vh1Jd9i5dKo
- The History of Quantum Mechanics
- Wolfram
- Nov 22, 2024
- for math students.
- new addition in great math software for coders.
- pywonderland.
- for coders. geometers.
- minor update.
- POV-Ray: Tutorial
- maybe working on real update.
- downloading povray now.
- Povray is 3d modeler, focus on rendering using ray-trace technique.
- it was state of the art for about 20 years since 1990s.
- what's a modern povray replacement
- https://x.com/i/grok/share/dK9AvC2eEzUcswYqmykwYnKWB
- Math, Geometry
- beautiful Islamic tiling patterns design, by ed-sandoval.
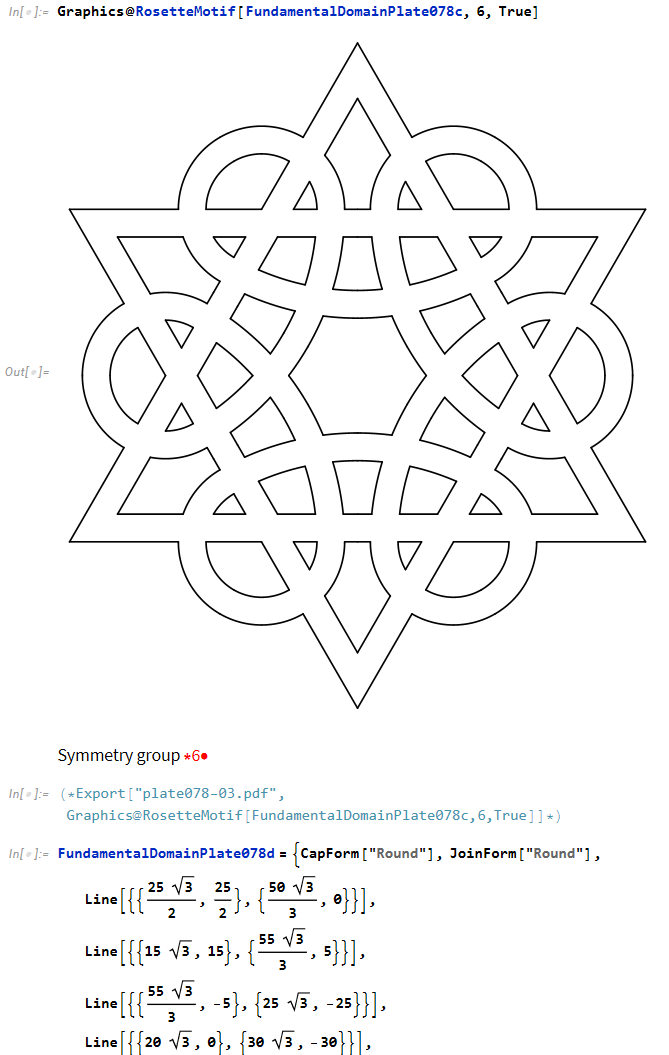


Theorem Proving in Lean 4
- Theorem Proving in Lean 4
- By Jeremy Avigad, Leonardo De Moura, Soonho Kong And Sebastian Ullrich.
- https://lean-lang.org/theorem_proving_in_lean4/
- having a lot fun reading this, lean lang book.
- very dense. reading chapter 2, a hour a day, for several days now.
- slowly and surely.
Some hardcore math science guys i recommend
Not in any order.
- Stephen Wolfram. physics math. https://x.com/stephen_wolfram
- Henry Segerman. geometry, math toys. https://x.com/henryseg
- Daniel Piker. geometry, architecture. https://x.com/KangarooPhysics
- Chaim Goodman-Strauss. geometry https://x.com/mathbun1
- Jonathan Gorard. physics. https://x.com/getjonwithit
- Dave Richeson. math. https://x.com/divbyzero
- Ed Pegg. math puzzles. https://x.com/mathpuzzle
- Vladimir Reshetnikov. cleo integrals. https://x.com/ereliuer_eteer
AlphaGeometry, AI Do Geometry Proof
- https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/
- 17 January 2024
- by Trieu Trinh and Thang Luong

Depth of Math and Despondency
- Every time i read math for a few days intensively, despondency sets in.
- You'll never know an iota of it, and there are a million better than you, and they are all mobbing toilets at MacDonalds.
- But, when i sometimes enjoy a brainless kungfu movie, do i ever worry about if am gonna ever watch all kungfu movies? No.
- So the key is, just enjoy.

repost.
finally done. updated from 1994.

Stephen Wolfram's articles, usually take several days full time to really dig thru. if u want to verify results to explore findings, take months or year.
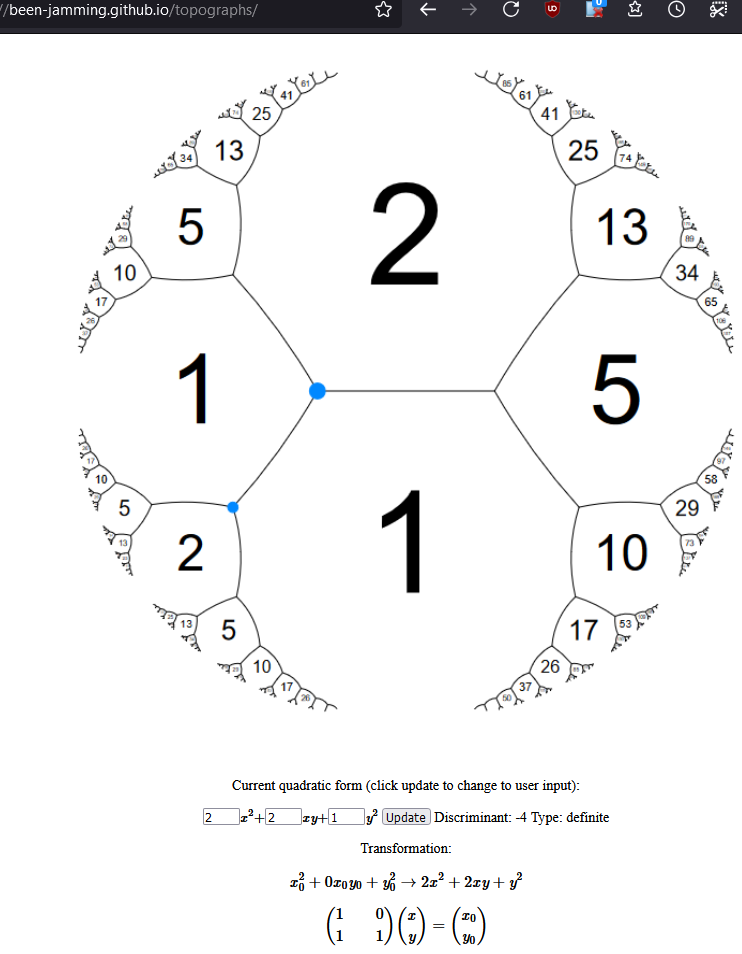
Conway Topograph
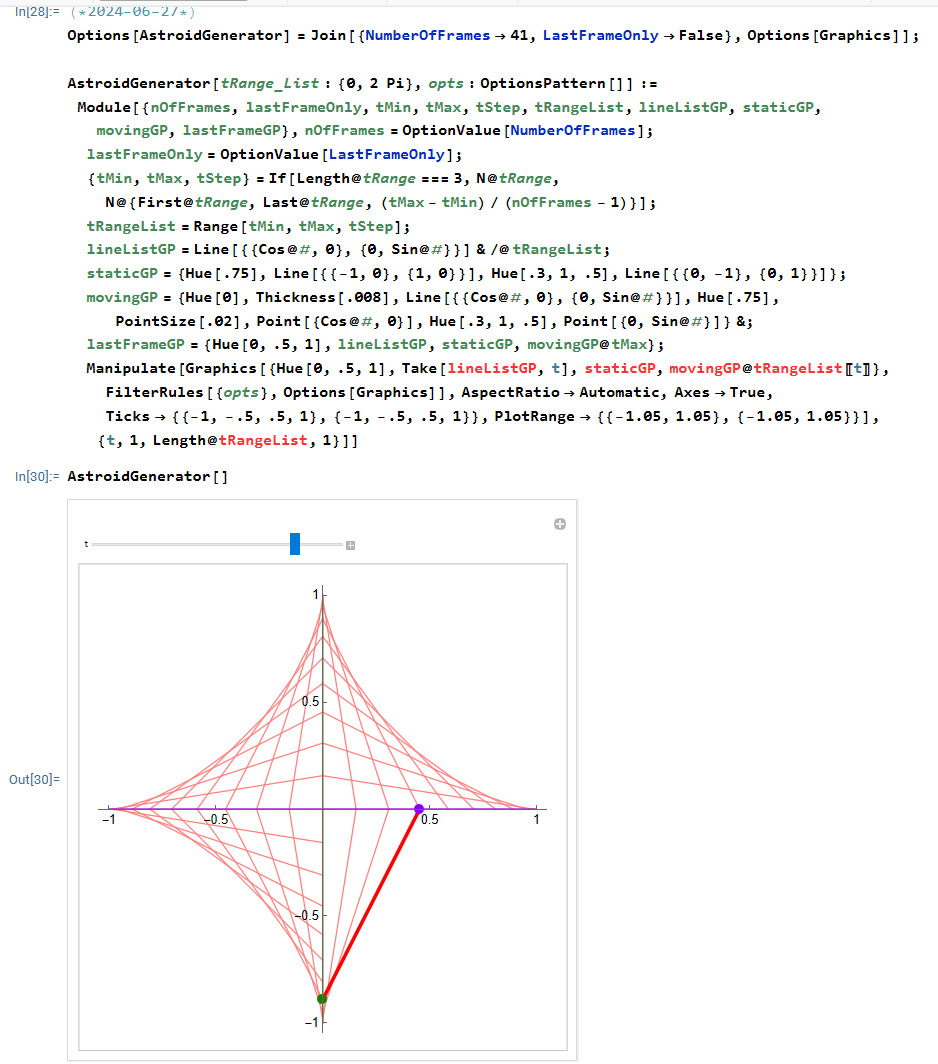
working on updating 30 years old WolframLang code that generates animation.
Ruled Surface, Mathematica Notes
new edition
now on github
now on github. updated 26-years-old code. still in heavy work. but putting on github now.
some random notes on mathematicians
some random notes
waiting for id
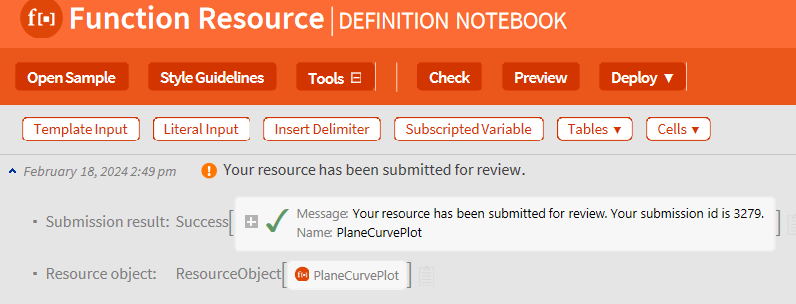
finally, published my PlaneCurvePlot to Wolfram Function Repository! this is updating a 30 years old package. After a week of remake. (was called ParaPlot.)


- Aggregation and Tiling as Multicomputational Processes
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2023/11/aggregation-and-tiling-as-multicomputational-processes/

- Games and Puzzles as Multicomputational Systems
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2022/06/games-and-puzzles-as-multicomputational-systems/

- Multicomputation with Numbers: The Case of Simple Multiway Systems
- By Stephen Wolfram.
- https://www.wolframphysics.org/bulletins/2021/10/multicomputation-with-numbers-the-case-of-simple-multiway-systems/
- A Class of Models with the Potential to Represent Fundamental Physics; The Updating Process for String Substitution Systems
- By Stephen Wolfram.
- https://www.wolframphysics.org/technical-introduction/the-updating-process-for-string-substitution-systems/
lots random reading notes
random list of great mathematicians
major update.
Carl Friedrich Gauss's Wives



- Remembering Doug Lenat (1950–2023) and His Quest to Capture the World with Logic
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2023/09/remembering-doug-lenat-1950-2023-and-his-quest-to-capture-the-world-with-logic/

- Untangling the Tale of Ada Lovelace
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2015/12/untangling-the-tale-of-ada-lovelace/
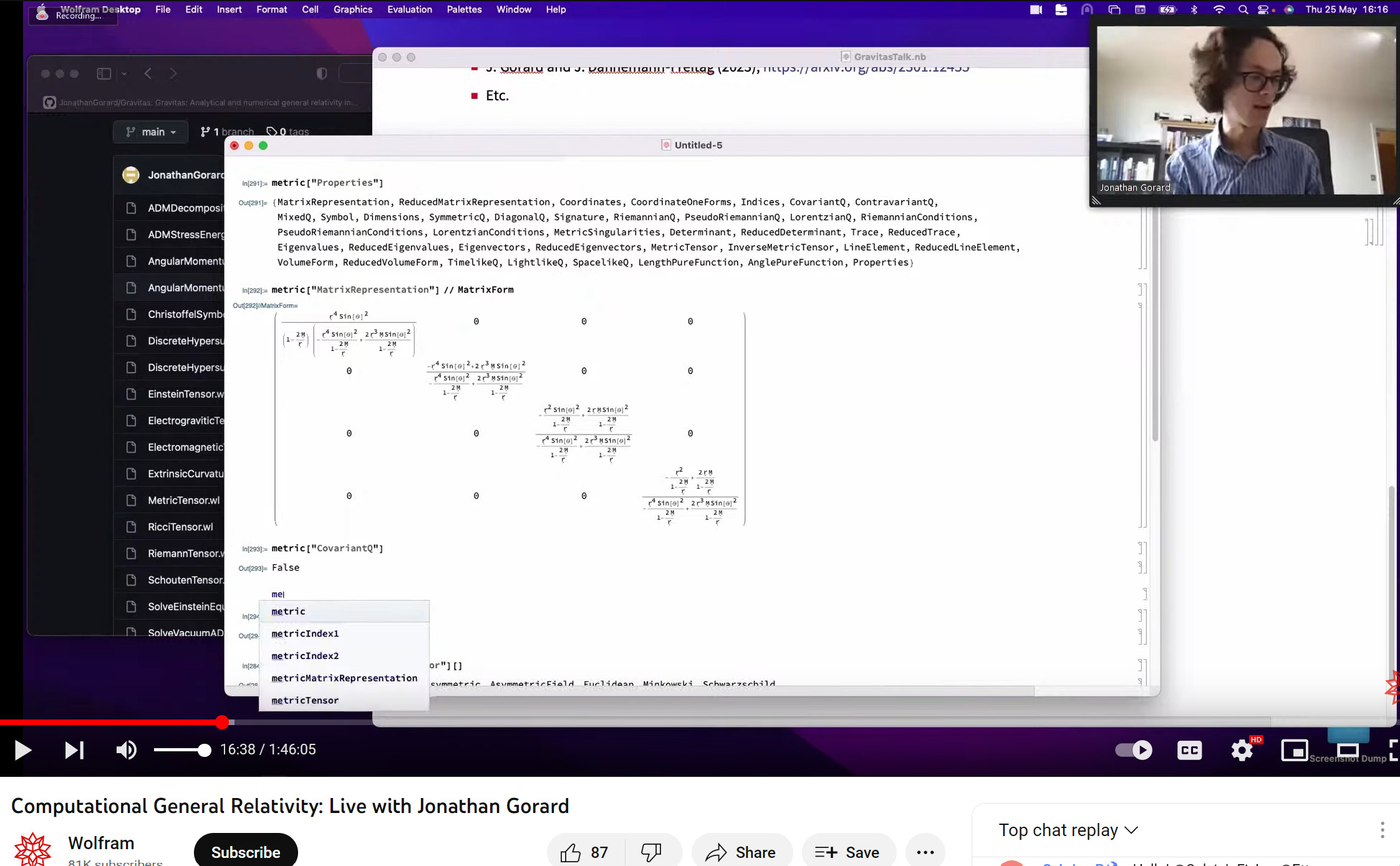
- https://youtu.be/_zuAg9oNifw
- Computational General Relativity: Live with Jonathan Gorard
- Wolfram
- Streamed live on May 25, 2023
here's WolframLang code, in plain text, rarely seen, as opposed to in notebook rendered math formula form. https://github.com/JonathanGorard/Gravitas
this allows you to do the unix tradition line-based diff and git version control. (big brain damage inherited from C and unix.)
but looking at it, i imagine it's auto generated from notebook. Writing math code in Mathematica notebook is just too feature rich and useful instead of coding it in plain text editor.
spectacular article.
- How Did We Get Here? The Tangled History of the Second Law of Thermodynamics
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2023/01/how-did-we-get-here-the-tangled-history-of-the-second-law-of-thermodynamics/
Homotopy Type Theory, Steve Awodey and Michael Warren
to watch
- https://youtu.be/-lZTnEgbVvI
- A visual introduction to the Hopf fibration
- OnePlusOneSpace
- Nov 9, 2022
cleaned up my old blogs, and made some into independent pages.
The gist here is to distill a math art into its algorithmic essence. By recursion or some encoding (such as math equation)
- lots updates and reorg Xah Math
- xtodo 2021-08-09 read Inversive geometry
- xtodo work on Math Graphics Gallery
- Coordinate Transformation
- Plane Curves Books
- Unicode: Math Font ℤ
- Unicode: Math Symbols π² ∞ ∫
- Unicode Symbol for “e.g.” (exempli gratia)
- HTML: XML Entities (Special Characters)
- Schmidt Arrangement, Algebra Integer, Gaussian Integer, Eisenstein Integer, Modular Group
- Complex Inversion
- Mobius Transformations
- Geometric Transformation on the Plane
- Helicoid-Catenoid
- Mathematical Simulation Ideas
Information Theory, Inference, and Learning Algorithms by David J C MacKay
Great Math Board Game Software updated
Freed Go. This guy now works for tesla. Amazing. When you compile math programs, since 1997, over the years i update them, and discover where these people went.
this is spectacular. Stephen Wolfram's personal stories of the greatest mathematicians, physicists, technologists of past 100 years
- https://youtu.be/H63LuAtRs4g
- History of Science and Technology Q and A (Jan. 27, 2021)
- by Wolfram
- Who Was Ramanujan?
- By Stephen Wolfram.
- https://writings.stephenwolfram.com/2016/04/who-was-ramanujan/
- Droste Effect with Mathematica
- By Jon Mcloone.
- http://blog.wolfram.com/2009/04/24/droste-effect-with-mathematica/
- The 2011 Mathematica One-Liner Competition
- By Christopher Carlson.
- http://blog.wolfram.com/2011/12/01/the-2011-mathematica-one-liner-competition/
parquet transform tiling. old links.
What Is Perspective Drawing
repost
some random page, minor edit
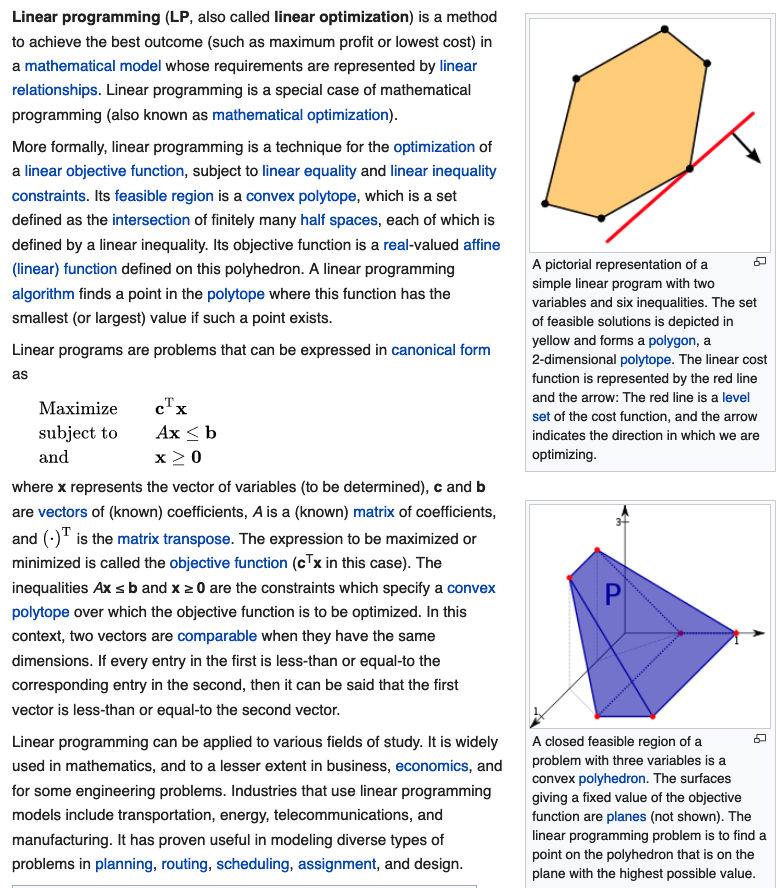
linear programing
Learned linear programing back in 1992 in college. Never encountered it since. But, about 2 years ago, when i was thinking about finding the optimal keyboard shortcut layout, it hit me, the problem is linear programing.
random article

good math book. What Is Mathematics? by Herbert Robbins , Richard Courant Buy at amazon
Math Mysticism: the Fibonaci Spiral Sham (2011)
Fibonaci is one of the undying myth in math.
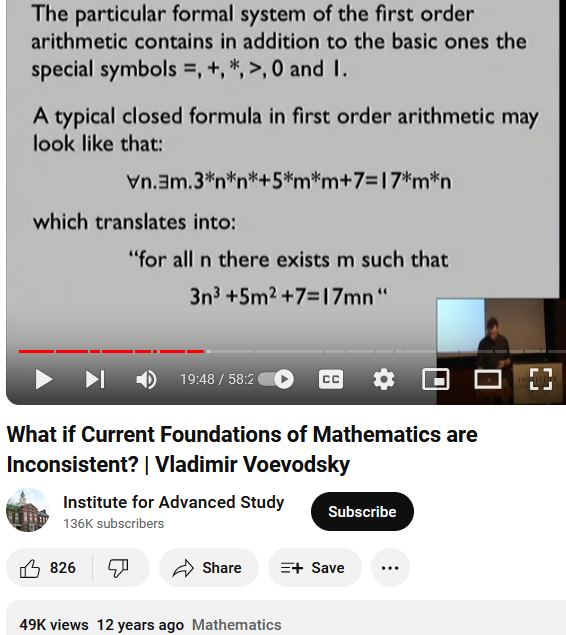
- https://youtu.be/O45LaFsaqMA
- What if Current Foundations of Mathematics are Inconsistent? | Vladimir Voevodsky
Fluid Simulation, added to Great Software for Cellular Automata
is there a name for a function that's dot product of more than 2 n-dimensional vectors?
for example , 3 vectors of 2D, it would be:
([a1,a2] , [b1,b2], [c1,c2] ) → (a1 * b1 * c1 + a2 * b2 * c2)

- God Created The Integers: The Mathematical Breakthroughs that Changed History
- By Stephen Hawking.
- Buy at amazon
Visualizing Quaternions
Geometer's Sketchpad, WebSketch
WebSketch, seems to be a new version of the Geometer's Sketchpad. http://geometricfunctions.org/fc/tools/
there are lots of them in past 10 years. see:
Town of the Great Math Hermit Alexander Grothendieck
Notes on the Riemann Hypothesis by Ricardo Pérez-Marco
Notes on the Riemann Hypothesis by Ricardo Pérez-Marco
1707.01770.pdf
via
https://twitter.com/johncarlosbaez/status/1164016020425543681
Octonions
- The Octonions
- By John C Baez.
- http://math.ucr.edu/home/baez/octonions/octonions.html
- (Published in Bull. Amer. Math. Soc. 39 (2002), 145-205. Errata in Bull. Amer. Math. Soc. 42 (2005), 213.)
pop cult of Feynman
God so many programer nerds are into Richard Feynman. I despise that guy, for no reason. it's like, any joe will shout Einstein when science is the topic. ok, Feynman is like top 10 physicist. but am not interested in physics. and whatever Feynman's math i have no interest.

i despise physicist. Whenever there is good piece of math, physicists ruin it.
#math John Milnor , big mathematician. one of his book is Topology from the Differential Point of View, 1965, John W Milnor
impredicative
Something that is impredicative, in mathematics, logic and philosophy of mathematics, is a self-referencing definition. Roughly speaking, a definition is impredicative if it invokes (mentions or quantifies over) the set being defined, or (more commonly) another set that contains the thing being defined. There is no generally accepted precise definition of what it means to be predicative or impredicative. Authors have given different but related definitions.
The opposite of impredicativity is predicativity, which essentially entails building stratified (or ramified) theories where quantification over lower levels results in variables of some new type, distinguished from the lower types that the variable ranges over. A prototypical example is intuitionistic type theory, which retains ramification so as to discard impredicativity.
Russell's paradox is a famous example of an impredicative construction—namely the set of all sets that do not contain themselves. The paradox is that such a set cannot exist: If it would exist, the question could be asked whether it contains itself or not — if it does then by definition it should not, and if it does not then by definition it should.
The greatest lower bound of a set X, glb(X), also has an impredicative definition: y = glb(X) if and only if for all elements x of X, y is less than or equal to x, and any z less than or equal to all elements of X is less than or equal to y. This definition quantifies over the set (potentially infinite, depending on the order in question) whose members are the lower bounds of X, one of which being the glb itself. Hence predicativism would reject this definition.[1]
2019-08-09 from Predicativism
am surprised, that the definition of infimum (or, e.g. shortest person in a room) is impredicative. and seems there is no predicative definition of them. and this seems to reduce the power of type theory drastically.
omniscience of math
god, please grand me omniscience of math.
while riding bike to pay rent yesterday, i thought about what'd happen if am omniscience of math. First, there are 6 Clay math price, each $1M reward. but as math omniscient, $6 millions is like 6 pennies on a dirty street.
with math omniscience, you now know the secret that's worth more than entire Google ($136 billion revenue in 2018). And you can break any secret message of any nation. Whatever US military spends in research in a decade, your knowledge is worth greater than that per second.
math omniscience also means, you are now the greatest mathematician. What you know is more than all mathematicians combined, dead or alive, infinitely times more. Quantum mechanics, cosmology. You KNOW the mysteries of the universe.
Math omniscience in a man. This is when, i wonder, if catastrophe might happen. You are now inhuman. You may no longer desire to eat.
stability of minimal surface
this is amazing! read the thread, by Daniel Piker: https://x.com/KangarooPhysics/status/1136306166349357058
that's amazing cuz it shows many popular minimal surfaces in math are not stable. I think it's rarely talked about. And he created a software that simulate soap film minimizing surface area.
And his blog is spectacular ( https://spacesymmetrystructure.wordpress.com ) i've known since 2011.
i think the stability issue is studied in stability theory, while minimal surfaces are differential geometry. These 2 are separate branches. Typically not studied together or at all both. Thus when we learn about minimal surfaces and soap film, talking about stability distracts.
a #geometry question i had for long. Given a bunch of points (that forms a surface), what's the (efficient) algorithm to triangulate them? any name i can search for?
answer: ball-pivoting algorithm. (thx to Daniel Piker)
readings about real number
Mathematician Adrien-Marie Legendre
truly despise the jargon injection surjection, created by Bourbaki

shape of space
if you want to understand this http://www.espaces-imaginaires.fr/works/ExpoEspacesImaginaires2.html there's a great book
applied group theory. 🤩
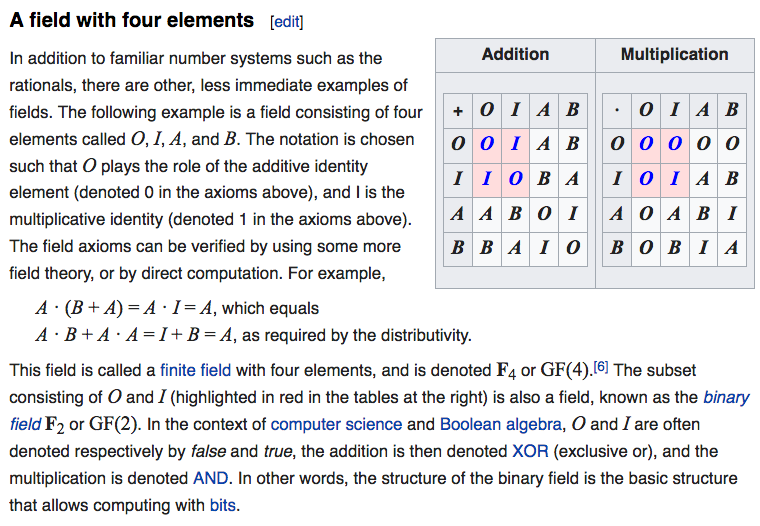
math. Field GF(4)
one of the smallest non-trivial field
Braid Group
cable knitting. Such intricacy, weave within weave.
was wondering if John C. Baez
https://twitter.com/johncarlosbaez
has written about math aspect of weaving. Searching braid theory baez, indeed!
Loop braid group
See also:

todo. read http://www.malinc.se/noneuclidean/en/poincaretiling.php
Great Software For 2D Visualization of Geometry
new app added
A Course In Universal Algebra, Burris, Sankappanavar
added a new text book. graduate level.
3 books i love. Now each on its own page.

Math, Algebra: on the Phraseology of X Over K, and What's Group Theory?
the supreme mystery of the universe, is math. note, not physics, quantum or blackhole crap.
u can write scifi about blackhole or quantum physics stuff, but u cant for math.
been slacking in the math department. Going to pick up again. Each day, i spend 1 hour reading math, and post whatever. Today, let's learn about “smooth map”.
this is logic, part of proof theory. this is what intent to learn in next 5 years, as opposed to category theory. (i got asked about the latter often, from programer idiots) [ twitter johncarlosbaez ] https://twitter.com/johncarlosbaez/status/1122976661132021760
Tennenbaum's theorem is a result in mathematical logic that states that no countable nonstandard model of first-order Peano arithmetic (PA) can be recursive (Kaye 1991:153ff).
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model. This theorem is an important tool in model theory, as it provides a useful method for constructing models of any set of sentences that is finitely consistent.
Finite model theory (FMT) is a subarea of model theory (MT). MT is the branch of mathematical logic which deals with the relation between a formal language (syntax) and its interpretations (semantics). FMT is a restriction of MT to interpretations on finite structures, which have a finite universe.
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics.
The most commonly studied formal logics are propositional logic, predicate logic and their modal analogs, and for these there are standard ways of presenting an interpretation. In these contexts an interpretation is a function that provides the extension of symbols and strings of symbols of an object language. For example, an interpretation function could take the predicate T (for “tall”) and assign it the extension {a} (for “Abraham Lincoln”). Note that all our interpretation does is assign the extension {a} to the non-logical constant T, and does not make a claim about whether T is to stand for tall and ‘a’ for Abraham Lincoln. Nor does logical interpretation have anything to say about logical connectives like ‘and’, ‘or’ and ‘not'. Though we may take these symbols to stand for certain things or concepts, this is not determined by the interpretation function.
An interpretation often (but not always) provides a way to determine the truth values of sentences in a language. If a given interpretation assigns the value True to a sentence or theory, the interpretation is called a model of that sentence or theory.
In mathematical logic, Lindström's theorem (named after Swedish logician Per Lindström, who published it in 1969) states that first-order logic is the strongest logic[1] (satisfying certain conditions, e.g. closure under classical negation) having both the (countable) compactness property and the (downward) Löwenheim–Skolem property.[2]
these shapes form hex stars. #geometry https://x.com/CGTNOfficial/status/1115445476537450496
- Too good to be Truchet
- By Colin Beveridge.
- http://chalkdustmagazine.com/features/too-good-to-be-truchet/
- Truchet
- By Cameron Browne.
- http://cambolbro.com/games/truchet/
- Truchet, Braille and Euler
- By Peter Rowlett.
- https://aperiodical.com/2010/02/truchet-braille-and-euler/
todo
Math and Illustrations
- Algorithmic Mathematical Art
- Art of M C Escher
- Escher Chameleon Polyhedron
- What is Technical Drawing, Descriptive Geometry, Projective Geometry, Linear Algebra
- Outline Rendering of 3D Models
- Autostereogram
- Visual Illusions
- Projective Illusion
- What Is Perspective Drawing
- Illustrating Geometry with POV-Ray
Geometric algebra
todo read
- Let's remove Quaternions from every 3D Engine (An Interactive Introduction to Rotors from Geometric Algebra)
- By Marc Ten Bosch.
- http://marctenbosch.com/quaternions/
i no unstand.
help:
- Linear and Geometric Algebra
- By Alan Macdonald.
- Buy at amazon
https://enkimute.github.io/ganja.js/examples/coffeeshop.html
- Geometric Algebra for Computer Science
- By Leo Dorst , Daniel Fontijne , Stephen Mann.
- Buy at amazon
some old articles.
- Mandelbrot Set Explained (no complex number needed)
- How Computing Science created a new mathematical style By Edsger W. Dykstra (EWD 1073)
- The TeX Pestilence: Why TeX LaTeX Sucks
- English/Chinese Math Terminology 中/英 数学术语
- What is the Difference of Russell's Logicism, Hilbert's Formalism, Axiomatic System?
- Math Notation, Computer Language Syntax, and the “Form” in Formalism (2003)
- Math Notation, Proof System, Computer Algebra, in One Language
- The Codification of Mathematics
- Math Terminology and Naming of Things (2004)
- Mathematical Notation: Past and Future
- Pattern Matching vs Grammar Specification (2008)
- A Notation for Plane Geometry
- State of Theorem Proving Systems 2008
- The Problems of Traditional Math Notation
- Notes On Plane Curves and Proofs
- Math Insight: Multiplication and Multiplicative Identity
Hyperboloid of Two Sheet http://VirtualMathMuseum.org/Surface/hyperboloid2/hyperboloid2.html
Dirac Belt Trick http://VirtualMathMuseum.org/Surface/dirac-belt/DiracBelt.html
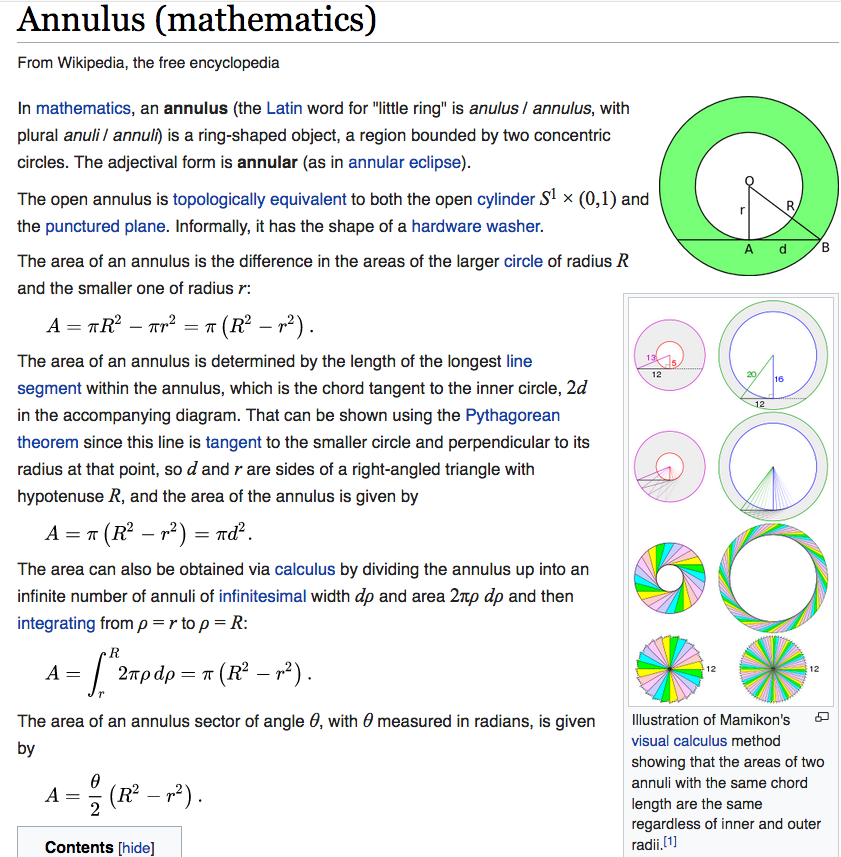
annulus, math
differential geometry site
been helping mat professors build differential geometry site.
latest are Soliton Surface and others, see:
- http://VirtualMathMuseum.org/Surface/hyperbolic_k1_sor/hyperbolic_k1_sor.html
- http://VirtualMathMuseum.org/Surface/two-soliton/two-soliton.html
- http://VirtualMathMuseum.org/Surface/three-soliton/three-soliton.html
- http://VirtualMathMuseum.org/Surface/four-soliton/four-soliton.html
visit the whole gallery at http://virtualmathmuseum.org/index.html
we've been working on it in past year.
See also: Wikipedia
graduate level differential geometry
math Three-Soliton Surface http://VirtualMathMuseum.org/Surface/three-soliton/three-soliton.htmlBreather Surface http://VirtualMathMuseum.org/Surface/breather/breather.html
Calculus, Gradient

Derivative and Jacobian Matrix
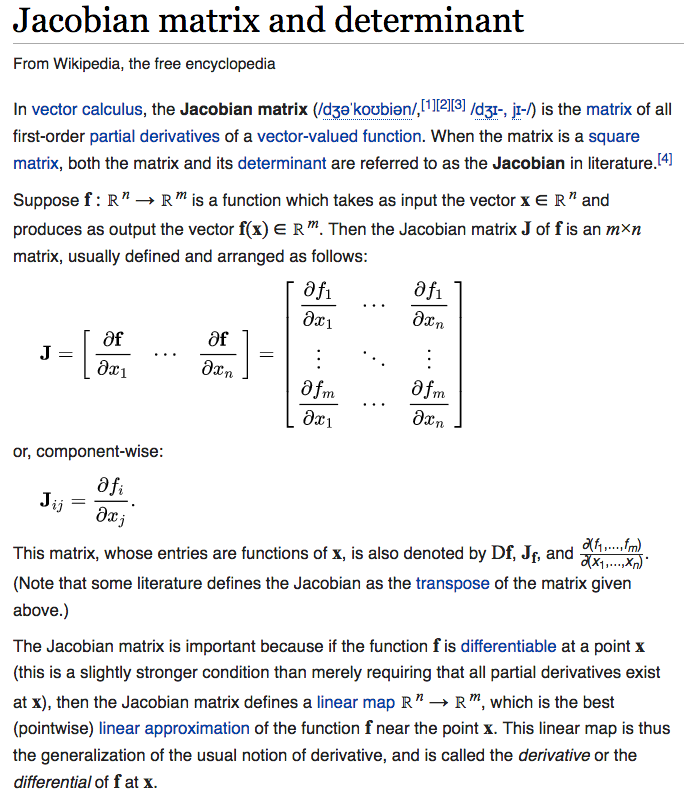
Jacobian matrix and determinant
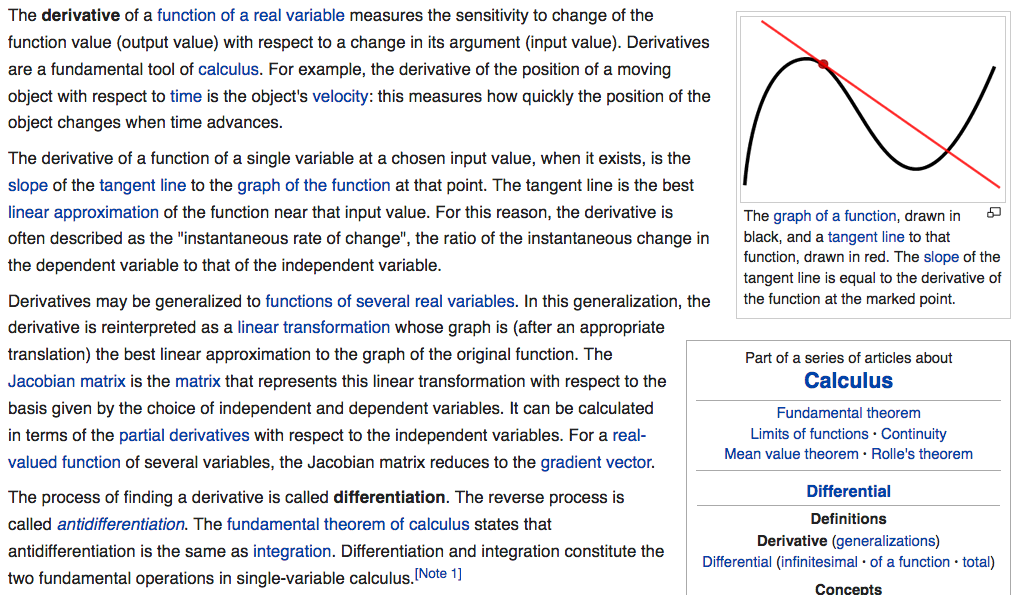
#math derivative. if you are rusty with calculus, or programer who never learned it, it's good time to revisit. join my journey. read my daily snippet, and lookup Wikipedia.
Wikipedia is usually chaotic, rambling on and on, touching highschool stuff to research stuff. if calculus is new to you, read textbooks. Here's Free Math Textbooks i verified quality. Free Math Textbooks
#math programers, if u haven't seen Conway's Game of Life yet, look into. it's eye opening. In 1990s, i spent years “playing” it. 1st deep theory you learn: deterministic system can be unpredictable. https://x.com/icm7216/status/1080209582041907200
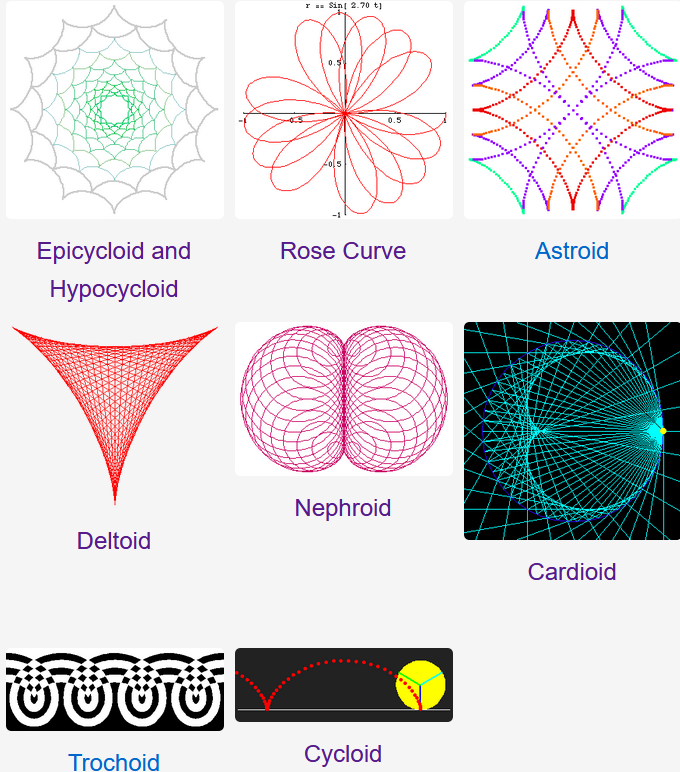
 WolframLang: Trochoid Plot 📦
WolframLang: Trochoid Plot 📦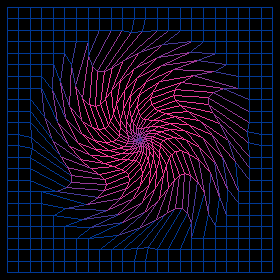 Geometry: Transformation of the Plane
Geometry: Transformation of the Plane Wolfram Language Plain Tiling Doc Draft
Wolfram Language Plain Tiling Doc Draft Penrose Tiling Deformation
Penrose Tiling Deformation Cleo Integrals in the Math StackExchange
Cleo Integrals in the Math StackExchange Stereographic Projection
Stereographic Projection Geometric Inversion, WolframLang Code
Geometric Inversion, WolframLang Code Algorithmic Mathematical Art
Algorithmic Mathematical Art Geometric Pattern on Sphere and Torus
Geometric Pattern on Sphere and Torus Doyle Spiral and Mobius Transformation
Doyle Spiral and Mobius Transformation Skew Dice But Fair
Skew Dice But Fair Knit Brain Hat
Knit Brain Hat Abacus
Abacus Math Art: Fractal Gears Clockwork
Math Art: Fractal Gears Clockwork Toroidal Earth Map
Toroidal Earth Map Reading Notes on Tilings and Patterns
Reading Notes on Tilings and Patterns Magic Polyhedrons
Magic Polyhedrons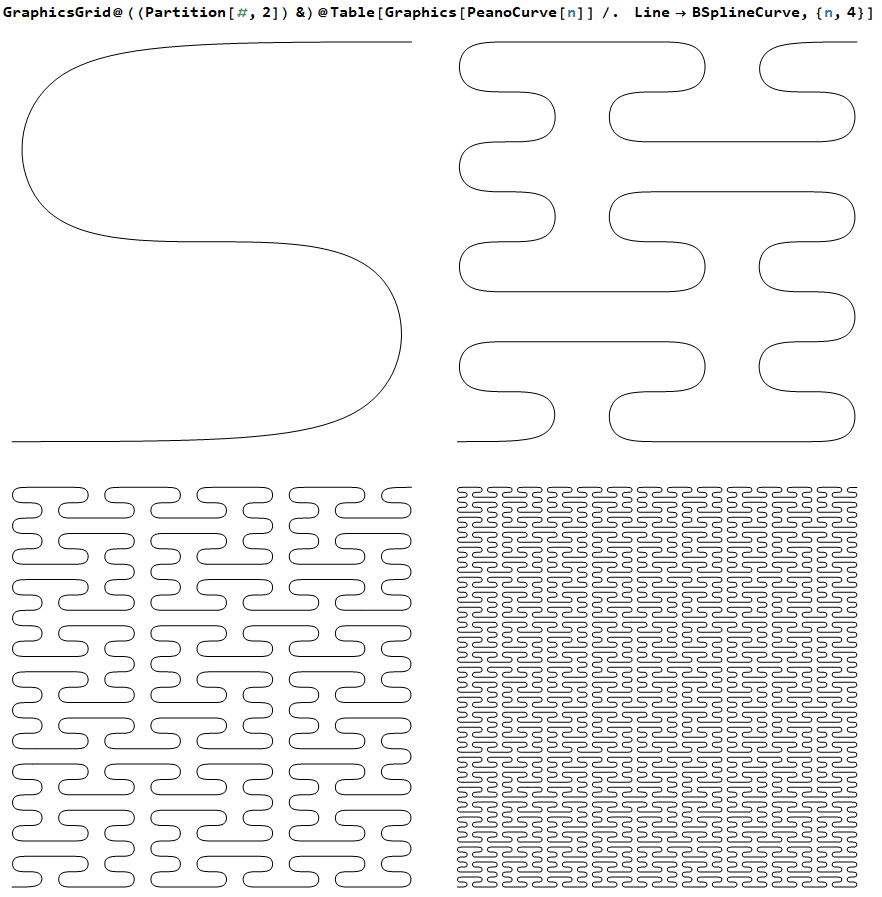 Space-Filling Curve
Space-Filling Curve uniform honeycomb
uniform honeycomb parametric cartoon curve
parametric cartoon curve Great Software For 2D Visualization of Geometry
Great Software For 2D Visualization of Geometry Software to Visualize 3D Geometry
Software to Visualize 3D Geometry Best Graphing Calculator
Best Graphing Calculator Go Board Game as Cellular Automata
Go Board Game as Cellular Automata Great Software for Cellular Automata
Great Software for Cellular Automata Great Software for Dynamical Systems
Great Software for Dynamical Systems Riemann Zeta Function
Riemann Zeta Function Knitting, Chinese Knots, Braid Theory
Knitting, Chinese Knots, Braid Theory Graph Theory Book
Graph Theory Book Visual Complex Analysis by Tristan Needham
Visual Complex Analysis by Tristan Needham Groups and Their Graphs by Israel Grossman and Wilhelm Magnus
Groups and Their Graphs by Israel Grossman and Wilhelm Magnus Roller Coaster Calculus
Roller Coaster Calculus