POV-Ray: Surface of Revolution and Prisms

This page is a short tutorial showing how to generate Surface Of Revolution shapes and Prism shapes. If you don't understand it, please see Intro to POV-Ray.

Lathe (Surface of Revolution)

Lathe with sharp edged profile

A surface of revolution can be made by the “lathe” keyword.

The lathe shape for the above ashtray is defined like this:

lathe { linear_spline 6 // number of vertexes below
 ,<0,0>, <4,0>, <4,2>, <3,2>, <3,1>,<0,1>
}

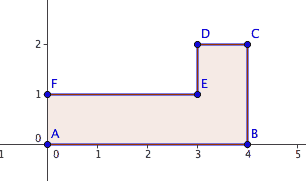
The coordinates are 2D coordinates, that specifies the key points of the shape's profile. POV-Ray will form the lathe shape by drawing lines connecting the given key points, then revolve the outline around the y-axes.

Lathe with smooth profile

Notice that the ashtray has a very angular shape. If you want to render a smooth vase, you will need a smooth outline. A solution for this is to use a smooth curve to fit the given vertexes. In place of the “linear-spline” keyword, POV-Ray provides quadratic_spline and cubic_spline. These are polynomials of 2 degrees and 3 degrees. POV-Ray also allows bezier_spline, that specify by curve by a point on the curve and a tangent at that point.

Here's a summary of the splines.

• linear_spline: 1st degree polynomial. 2 points defines a segment, which is just a line passing thru the two points.
• quadratic_spline: 2rd degree polynomial. 3 points defines a segment. To determin the curve that connects point P[n] and P[n+1], POV-Ray uses points P[n],P[n+1],P[n+2]. Suppose your last point is P[m]. In order to compute the curve between P[m-1] and P[m], POV-Ray needs another point. So, when using quadratic_spline, you need to add one extra point at the end of your point list.
• cubic_spline: 3rd degree polynomial. 4 points defines a segment. To determin the curve that connects point P[n] and P[n+1], POV-Ray uses points P[n-1],P[n],P[n+1],P[n+2]. Notice that it uses a point before P[n]. So, to compute the first segment in your point list, POV-Ray will need one extra control point. Similarly, POV-Ray will need one extra control point to compute the last segment. So, to use cubic_spline, you need to add one extra point before your point list, and one extra point at the end of your list.
• bezier_spline: Tangent based curve. For each point A on the profile curve, another point B is given, where the vector B-A is the vector tangent at A.

lathe { cubic_spline 8,
  <-1,0>,<0,0>, <4,0>, <4,2>, <3,2>, <3,1>,<0,1>,<-1,1>
…
}

Note that when you use cubic_spline, you have to add 1 more vertex to the beginning of your outline and 1 more vertex to the end, because cubic needs 3 neighboring points to come up with a curve that passes thru a given point.

2.4.1.7 Lathe

Note: another way to do surface of revolution is by using the “sor” keyword, which stands for Surface Of Revolution. However, sor requires that its outline curve be a function (i.e. one value per height and no self crossing), so it is less powerful than “lathe”. For example, you cannot use “sor” to generate a torus, or a bowl. The only advantage of “sor” is that it is faster to render.

2.4.1.12 Surface of Revolution

Prisms

A surface of revolution is made by revolving a outline thru a axis. A prism is made by extruding a outline in the direction of a axis.

In POV-Ray, lathe and prism have similar syntax. Here's a example of extruding a simple parallelogram:

prism {
  linear_sweep
  linear_spline
  0, // starting height
  .6, // ending height
  5, // the number of coordinates below
  <0,0>, <1,0>, <2,1>, <1,1>,<0,0>
// note the extra last point to close the outline
}

If your outline crosses itself, POV-Ray will automatically determine the inside/outside. Example:

You can have multiple outlines within a single prism{} statement. When a point is repeated, POV-Ray considers it as the ending of the first outline, and the next point (or, after the control points, if any) will be the beginning of another outline. When all the outlines are done, a simple inside/outside algorithm will determine which sections of the outline are filled.