xtodo Wolfram language

xtodo
xtodo 
(* 
Wolfram language
why in xah emacs mode, this no work
 *)

Get[ "InvertCircle.wl" ]

(* but this works *)

Get["xxss.wl" ]

Get[ "InvertCircle.wl" ]
Get["xxss.wl" ]
Directory[]
(* c:\Users\xah\git\InvertCircle *)
xtodo 
(* gralist is a list of graphics *)

MapIndexed[
Function[{xx,ii}, Export[StringTemplate["xx_``.svg"][ii[[1]]] , xx ]]
, gralist]
xtodo 
CirclePoints
xtodo
xtodo
xtodo
xtodo
xtodo
xtodo 
(* when there are multiple rules, the more specific is applied first? *)
ReplaceAll[ {1, {2, {3, {4}}}},
{
{2,_} -> x,
{1,{2,_}} -> y
}
]
(* y *)

(* when there are multiple rules, the more specific is applied first? *)
ReplaceAll[ {1, {2, {3, {4}}}},
{
{2,_} -> x,
{3, {4}} -> y
}
]
(* {1, x} *)
$CharacterEncodings
$SystemCharacterEncoding
$SystemCharacterEncoding = "UTF-8";
x = "i ♥ cats and dogs"
(* move all 0 to the left of 1 *)
ReplaceAll[
{3, 1, 1, 0, 0, 3, 1, 1, 0, 0} ,
{head___,
Pattern[dots, Longest[ 1.. ] ],
Pattern[balls, Longest[ 0.. ] ],
tail___} -> {head , balls , dots , tail}
]

(* {3, 0, 0, 1, 1, 3, 1, 1, 0, 0} *)

(* look into why don't do the rest *)

need work

wstp wolfram symbolic transfer protocol

to read

function repo

paclet package repo

programatically turn a expression into a function

th[ft_Function , xrest___] :=
tt[ With[{expr179= ft@argHq2Ky},
With[{x881= First@ expr179, y804= Last@ expr179},
{x881, y804} /. argHq2Ky -> #1 ] ] ,
 xrest] /;
SameQ[Length@ ft, 2];
(* \|01f469 *)

StringLength[ FromCharacterCode[{128105, 8205, 128300}]] === 3
(* StringLength["\|01f469"] *)

pattern matching issues

assume just 1 rule:

Replace[ f[x,x] , {x -> 3, y -> 4}, {1, Infinity  } ]

(* f[3, 3] *)
(*
WolframScript does not behave the same as notebook.
In notebook, these eval correctly.
in WolframScript, they do not.
*)

StringCases[ "αβ🌞ab", StringExpression[ LetterCharacter.. ] ]
(* {Î, Î, ð, ab} *)

StringCases[ "πσ", StringExpression[ "ΠΣ" ], IgnoreCase -> True ]
(* {} *)

What's the difference between Hold, HoldForm, Unevaluate

Attributes[ CompoundExpression ]
(* {HoldAll, Protected, ReadProtected} *)

(* CompoundExpression *)

FullForm[  a;b;c ]
(* FullForm[c] *)

FullForm[ Hold[ a;b;c ] ]
(* FullForm[Hold[a; b; c]] *)

FullForm[ HoldForm[ a;b;c ] ]
(* FullForm[HoldForm[a; b; c]] *)
Mathematica save to html 2022-05-14
Mathematica save to html 2022-05-14
Wolfram exe 2022-05-14
Wolfram exe 2022-05-14 
# list file path of WolframLang
Get-Command wolframscript.exe | Format-List Source

# on windows, it's usually at
# C:\Program Files\Wolfram Research\WolframScript\wolframscript.exe

on linux or MacOS, type which wolframscript

2022-05-13, commented on
https://reference.wolfram.com/language/ref/ParametricPlot.html

the two examples with Exclusions, has no effect.

ParametricPlot[{Tan[u], u}, {u, 0, 2 Pi},
 Exclusions -> Range[Pi/2, 2 Pi, Pi]]

ParametricPlot[{Tan[u], u + v}, {u, 0, 2 Pi}, {v, 0, 1},
 Exclusions -> {u == Pi/2, u == 3 Pi/2}, Axes -> None]

sequence specification:

All
all elements
None
no elements
n
elements 1 through n
UpTo[n]
elements 1 up to at most n, as available
-n
last n elements
{n}
element n only
{m,n}
elements m through n inclusive
{m,n,s}
elements m through n in steps of s

Drop

Replace

Implementing Contour Plot 3D

This is interesting and hard to implement. The function takes a 3D array. Then, create a surface that basically connects similar values together. Say, you have a 3d array, each value is a number from 1 to 1000.

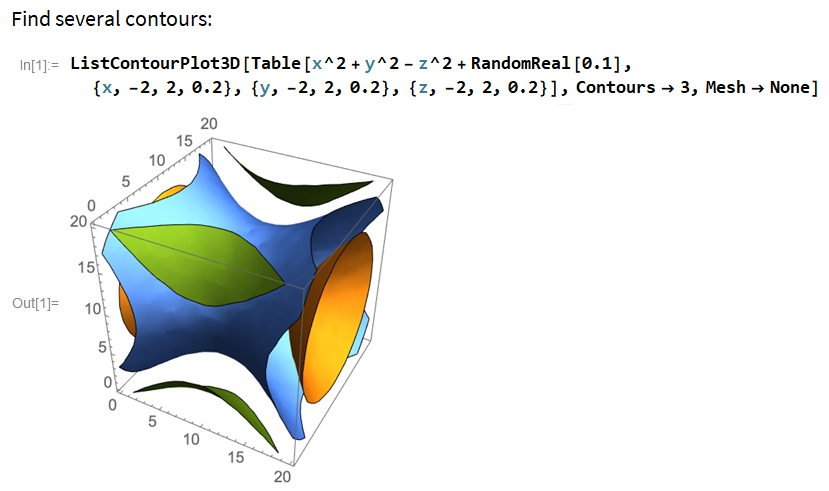
Wolfram Language ListContourPlot3D zZ6nb
http://reference.wolfram.com/language/ref/ListContourPlot3D.html

ListContourPlot3D[array] generates a contour plot from a three-dimensional array of values. ListContourPlot3D[{{x1, y1, z1, f1}, {x2, y2, z2, f2}, ...}] generates a contour plot from values defined at specified points in three-dimensional space.

needs computational geometry knowledge to implement this.

actually this post should be in #programing .

first hard problem is , imagine you have a 3d matrix, how to you find out the indexes for elements in the matrix that have the same value? (let's assumes all the values are integers. forget about float or approximately equate as required) this is non-trivial to implement it efficiently.

second non-trivial problem: once you found indexes that have the same value, you need to determine if they are adjacent in 3D space. Basically, the indexes for each el in matrix is its coordinate. If 2 same value are not connected, you don't draw surface.

3rd hard problem is, given a bunch of points in 3d space forming a surface, you need to triangulate them into a mesh in order to draw the surface. classic computational geometry problem.

omg this is one level harder. computational geometry! once you have a surface, and given a plane intersecting it. you need to draw curves on the plane to show the intersection (like cross section). The plane can actually be ANY surface!

Wolfram Language ListSliceContourPlot3D f9wN5
http://reference.wolfram.com/language/ref/ListSliceContourPlot3D.html

one can get a phd in computational geometry just for creating a algorithm to solve this problem efficiently. i presume it's mostly solved problem.