Xah Math Blog Archive 2018-01
monty hall problem

#math #probability. The famous Monty Hall problem, Marilyn vos Savant, one with highest IQ. Am still trying to resolve this paradox from philosophical aspect.
Say we are told that a woman has two children. If we ask whether either of them is a girl, and are told yes, what is the probability that the other child is also a girl? Considering this new child independently, one might expect the probability that the other child is female is 1/2. But by building a probability space (illustrating all possible outcomes), we see that the probability is actually only 1/3. This is because the possibility space illustrates 4 ways of having these two children: boy-boy, girl-boy, boy-girl, and girl-girl. But we were given more information. Once we are told that one of the children is a female, we use this new information to eliminate the boy-boy scenario. Thus the probability space reveals that there are still 3 ways to have two children where one is a female: boy-girl, girl-boy, girl-girl. Only ⅓ of these scenarios would have the other child also be a girl.[17] Using a probability space, we are less likely to miss one of the possible scenarios, or to neglect the importance of new information. For further information, see Boy or girl paradox.
This technique provides insights in other situations such as the Monty Hall problem, a game show scenario in which a car is hidden behind one of three doors, and two goats are hidden as booby prizes behind the others. Once the contestant has chosen a door, the host opens one of the remaining doors to reveal a goat, eliminating that door as an option. With only two doors left (one with the car, the other with another goat), the player must decide to either keep their decision, or switch and select the other door. Intuitively, one might think the player is choosing between two doors with equal probability, and that the opportunity to choose another door makes no difference. But probability spaces reveal that the contestant has received new information, and can increase their chances of winning by changing to the other door.[17]
2018-12-30 Randomness
super beautiful. #math #geometry https://x.com/TilingBot/status/1079505991048282112
idiotic math jargons
2 idiotic math jargon are: Probability Mass Function and Probability Density Function. They should be called Discrete Probability Distribution Function and Continuous Probability Distribution Function.
idiotic math jargon: Stochastic Process. It has no mathematical meaning, opaque, and also misleading. Stochastic Process force math to be viewed as a “process”, but the very nature of math is inert and static.
another idiotic math jargon is Monte Carlos method. It has no mathematical meaning, and is opaque. Better is random element method.
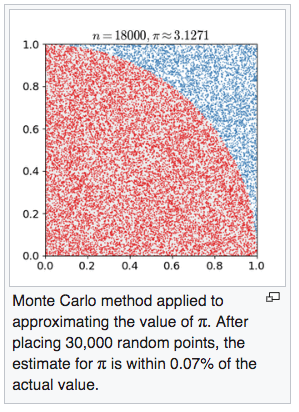
This is the so-called Monte Carlos method of computing π. Area of 1/4 circle is (pi r^2)/4. Area of the square is r^2. Ratio is π/4. Throw darts on it, then count dots inside / total, times 4, = π. Silly? why not just use grid points instead of random dots?
Introduction to Probability
2 dices. throw 24 times. what is the probability it turns out at least 1 double 6? Programers, go write code to simulate it. But you can never be sure. Mathematician can.
Meromorphic function and Holomorphic function
#math #geometry Meromorphic function should be called Pinholed Analytic function, or just Pinholed function. the term “Holomorphic function” should be ban'd, replaced by Analytic Function.
#physics Wave–particle duality, still not understood
how many beatings does it take? Wave–particle duality
Wave–particle duality is the concept in quantum mechanics that every particle or quantum entity may be partly described in terms not only of particles, but also of waves. It expresses the inability of the classical concepts “particle” or “wave” to fully describe the behavior of quantum-scale objects. As Albert Einstein wrote:[1]
It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do.
Through the work of Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr and many others, current scientific theory holds that all particles exhibit a wave nature and vice versa.[2] This phenomenon has been verified not only for elementary particles, but also for compound particles like atoms and even molecules. For macroscopic particles, because of their extremely short wavelengths, wave properties usually cannot be detected.[3]
Although the use of the wave-particle duality has worked well in physics, the meaning or interpretation has not been satisfactorily resolved; see Interpretations of quantum mechanics.
Bohr regarded the “duality paradox” as a fundamental or metaphysical fact of nature. A given kind of quantum object will exhibit sometimes wave, sometimes particle, character, in respectively different physical settings. He saw such duality as one aspect of the concept of complementarity.[4] Bohr regarded renunciation of the cause-effect relation, or complementarity, of the space-time picture, as essential to the quantum mechanical account.[5]
Werner Heisenberg considered the question further. He saw the duality as present for all quantic entities, but not quite in the usual quantum mechanical account considered by Bohr. He saw it in what is called second quantization, which generates an entirely new concept of fields which exist in ordinary space-time, causality still being visualizable. Classical field values (e.g. the electric and magnetic field strengths of Maxwell) are replaced by an entirely new kind of field value, as considered in quantum field theory. Turning the reasoning around, ordinary quantum mechanics can be deduced as a specialized consequence of quantum field theory.[6][7]
is 0 a natural number?
https://x.com/divbyzero/status/1063441410811199488
saw this late. 0 is the most unnatural, by definition! afaik, 0 didn't come into being until thousands of years of humanity. Between 0 and ∞, they are the 1st artificial number! ☺
Robert Langlands won 2018 Abel Prize
#math Robert Langlands won 2018 Abel Prize ($740k) for his work that “relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles.” Langlands program
Synthetic geometry, absolute geometry, ordered geometry, incident geometry, tarski's axioms
Geometry, as presented by Euclid in the Elements, is the quintessential example of the use of the synthetic method. It was the favoured method of Isaac Newton for the solution of geometric problems.
Synthetic methods were most prominent during 1800s when geometers rejected coordinate methods in establishing the foundations of projective geometry and non-Euclidean geometries. For example the geometer Jakob Steiner (1796 to 1863) hated analytic geometry, and always gave preference to synthetic methods.
Karl von Staudt showed that algebraic axioms, such as commutativity and associativity of addition and multiplication, were in fact consequences of incidence of lines in geometric configurations. David Hilbert showed[8] that the Desargues configuration played a special role. Further work was done by Ruth Moufang and her students. The concepts have been one of the motivators of incidence geometry.
Tarski's axioms Tarski's axioms that turns synthetic #geometry to its actual nature, formal logic
magic of dot product
#math dot product https://en.wikipedia.org/wiki/Dot_product a magic operation that formalize vector space with angle n length: inner product space
- A:=(a1,a2)
- B:=(b1,b2)
- A.B:=a1*b1+b2*b2
the magic is this: a1*b1+b2*b2 “happens to” == √(a1^2+a2^2)*√(b1^2+b2^2)*cos[θ] by trig
See also: Free Math Textbooks
so, can anyone explain what's multilinear algebra? #math differential #geometry
last year (2017) i spend few hours per day reading math. gonna start to do that again.
here's several Free Math Textbooks i've verified for quality Free Math Textbooks if you not familiar, refresh your calculus, then linear algebra. They are the most fundamental
smooth function
In mathematical analysis, the smoothness of a function is a property measured by the number of derivatives it has that are continuous. A smooth function is a function that has derivatives of all orders everywhere in its domain.
continuous function
In mathematics, a continuous function is a function for which sufficiently small changes in the input result in arbitrarily small changes in the output. A continuous function with a continuous inverse function is called a homeomorphism.
measure theory and modern math
measure theory. basically, a modern version of the concept of length, area, volume Measure (mathematics)
the writing style of #math since 1990s, even its body, is about make it logical statements from set theory
it's all great, until you learned, there are a few math foundations, and different logic systems, and logic used in most traditional math is so bad that it cannot be computerized. thus Homotopy Type Theory only began in ~2010
Lebesgue's Universal Covering Problem
just read john baez's fascinating article on Lebesgue's Universal Covering Problem https://johncarlosbaez.wordpress.com/2015/02/03/lebesgues-universal-covering-problem-part-2/
Alex's Adventures in Numberland
found this math book Alex's Adventures in Numberland by Alex Bellos Buy at amazon year 2011. good reviews
Algorithmic Mathematical Art, hits hackernews
https://news.ycombinator.com/item?id=18397804
i think that article hit hackernews for the 3rd times in past decade+.
math, programing, proof systems
i haven't done any math in 2018. sad. but i hope to start again. and in next 2 months, create js code lib plotting plane curves. in 2017, was spending like 4 hours a day reading math. differential geometry and others. really missed that.
1 interesting thing about math is that, ever since 1990s, i tried to write math by programing code. always got frustrated. lots problems, between syntax, programing code, and math semantics (i.e. set theory). Turns out, this is a major prob, only in recently years there's solution. e.g. homotopy type theory.
in computer code, we can define functions or variable. But try to define definition of group, or even a set. you have problems. One gist of problem to illustrate is: there exist. This phrase, is a concrete example core problem of defining math (set theory) by algorithm.
when you try to say write math learning notes as computer programs, e.g. you just learned linear function. Now, try to express that concept in programing language. you start to get a sense of the probles. and this is what i mean, was what i was trying to do in 1990s.
the problem here, is a inter-mesh of so called foundation of math, logic, algorithm, and notation/syntax, as well as programing language features, such as pattern matching, logic oriented languages, etc. In 1 word, it's what automated/computer-aid proof system researh since 60s.
math is about what is. programing is how to. it's definition vs algorithm. On the surface, you'd think both are utmost precise and logic. One should easily turn entire body of math into code, or vice versa. In reality, it's proof system/math foundation research in past decades.
it's only in past decade or so, there's a glimmer of hope that math/code can be unified. e.g. look into howard curry isomorphism, homotopy type theory. (btw, if u r programer or haskell fan, lol. it's not what u think. shuddaFU. i no wanna hear what u have to say.)
it's only in past decade or so, there's a glimer of hope that math/code can be unified. e.g. look into howard curry isomorphism, homotopy type theory. (by the way, if you are programer, or haskell fan, lol, no u. it's not what you think. and your wishes are not true. STFU. i no wanna hear what u have to say.)
old article. Introduction to Symmetry and wallpaper groups to laymen Introduction to Symmetry
Non-Archimedean geometry
- Yifeng Liu wins prestigious award in mathematics
- By Maeve Forti.
- https://news.yale.edu/2018/10/25/yifeng-liu-wins-prestigious-award-mathematics
his publications https://gauss.math.yale.edu/~yl2269/
Chinese nuclear physicist 何泽慧 He Zehui (1914 to 2011)
iff or not to iff
Math copyediting question: is it “if and only if” or “if, and only if,” (i.e., commas or no commas?) (I know I could avoid the issue by using iff…)
2018-09-24 from mathematician Dave Richeson https://x.com/divbyzero/status/1044209941064617984
“if and only if” of course. That's one unit.
i used to like iff when i was student ~92. now i find that annoying, as if if typo. am with @henryseg, prefer the symmetric ⇔. But i find that i prefer it too much, that am rly going for total computerized math by logical symbols. as i learned, has lots of its own problems. ☺
See Also: John Carlos Baez's discussion
[ twitter johncarlosbaez ] https://twitter.com/johncarlosbaez/status/1043975994246291456
geometry Steiner chain
- Card Shuffling Visualizations
- By Roger Antonsen.
- http://archive.bridgesmathart.org/2018/bridges2018-451.pdf
math John Conway Free will theorem
“if we have a free will in the sense that our choices are not a function of the past, then, subject to certain assumptions, so must some elementary particles”
- John Conway – discovering free will (part I)
- By Rachel Thomas.
- https://plus.maths.org/content/john-conway-discovering-free-will-part-i
Great Math Software: Polyhedrons and Polytopes
minor update. If you have a old Mac from 1990s to 2000s, check out that old math software page.
Great Math Software: Tilings and Patterns
added a new tiling app for Mac

Magic Polyhedrons (Rubik Cube) (updated)
Great Software for Plane Geometry (updated)
obsolete math software, 1990s to 2005
revisiting and updating my page on list of great math software, mostly from 1990s. Many, are from hobbyists, truly great programs. Times flies. People get old. Many are not updated. Many websites gone. And many Java applets, as relics of tech progress.
It's like, right now you are hot into programing, machine learning, this or that. 10 or 20 years later, you might be something else, or puffed off. You look into the ebb and flow of each human animal life activity as cellular automata, it'd be something.
for nostalgia, here's list of obsolete math software. 1990s to ~2005. In Mac classic, Java, Flash. Old Math Software
Great Math Software: Tilings and Patterns (major update)
preorder, partial order, total order
The original concept of totally ordered set or order, still dominant today, obeys a bunch of rules:
- reflexivity: x≤x
- transitivity: x≤y and y≤z imply x≤z
- antisymmetry: if x≤y and y≤x then x=y
- trichotomy: for all x,y we either have x≤y or y≤x.
The real numbers with the usual ≤ obeys all these. Then people discovered many situations where rule 4 does not apply. If only rules 1-3 hold they called it a partially ordered set or poset. Then people discovered many situations where rule 3 does not hold either! If only rules 1-2 hold they called it a preordered set or preorder.
Category theory teaches us that preorders are the fundamental thing: see Lecture 3. But we backed our way into this concept, so it has an awkward name. Fong and Spivak try to remedy this by calling them posets, but that's gonna confuse everyone even more! If they wanted to save the day they should have made up a beautiful brand new term.
2018-03-29 by John Baez from https://forum.azimuthproject.org/discussion/comment/16083/#Comment_16083
category theory online course
So, am taking a online course of category theory, lead by famous mathematician and theoretical physicist John Baez.
the home page is at https://forum.azimuthproject.org/discussion/1717/welcome-to-the-applied-category-theory-course
the textbook is: https://arxiv.org/abs/1803.05316
local mirror category_theory_brendan_fong_david_spivak_2018-03.pdf
some great math related JavaScript site added.
Using Neural Net to Create New Knitting Patterns
Quite amazing.
https://x.com/JanelleCShane/status/964945688613199872
by Janelle Shane
random sequence, not mathematically defined
it's interesting, that the concept of random number, or random sequence, is actually undefined in math, because it is impossible to define mathematically.
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words “let X1,…,Xn be independent random variables…”. Yet as D. H. Lehmer stated in 1951: “A random sequence is a vague notion… in which each term is unpredictable to the uninitiated and whose digits pass a certain number of tests traditional with statisticians”.[1]
Axiomatic probability theory deliberately avoids a definition of a random sequence.[2] Traditional probability theory does not state if a specific sequence is random, but generally proceeds to discuss the properties of random variables and stochastic sequences assuming some definition of randomness. The Bourbaki school considered the statement “let us consider a random sequence” an abuse of language.[3]
[2018-03-19 Random sequence]
follow xah
follow me on my new mastodon account at https://mstdn.io/@xahlee and on reddit https://www.reddit.com/user/xah
Philosophy of Math: Logicism, Formalism, Intuitionism, and Category Theory
the 3 philosophy of math of 1900s are: (1) logicism. Math is pure derivation of logic. (2) Hilbert's formalism. Math is just bunch of fomulaic symbols. No meaning. (3) intuitionism. Math is mind's construction.
these 3 schools are the basis of foundations of math. Each has its problems. logic became formal (i.e. symbolic) logic, which is basically formalism. They in turn, became constructivism (a variation of intuitionism), so it can run by computer.
comment at https://plus.google.com/+XahLee/posts/LZJPcj4KGRB
here's my comment to mathematician john baez:
thanks for correction.
i've always wondered what's the difference of logicism and formalism. Back in 1990s, I was introduced to them by Russell. (my top 3 fav author) Tried to read about them now and then. In 2000s, wikipedia is still not great, but in past year, i read a lot math again, and i seem to get some understanding. Is my characterization roughly correct?
i never cared about intuitionism, until now, and now i very much appreciate constructivism. As i understand, it is what mechanical manipulation can actually build.
PS few days ago i tried to read wikipedia about category theory again. Again, came away as incomprehensible abstraction. Meant to write a rant about it… but here's a gist…
so i spend half hour thinking, what does abstraction mean? After all, numbers 1 2 3 ... are abstraction to begin with. But then we have equations, such as 2*x+3 = 4, which is abstraction of description of math problems. Then, abstract algebra and 1800s's math, are the 2nd stage of abstraction. e.g. abstract algebra came from the systematic formal maniputlation of equations. And likewise stuff in algebraic geometry e.g. variety, and differential geometry geometry e.g. manifold, and so on in other branches of math.
Then, what's the next level abstraction? I'm thinking, scheme and sheaf etc (which i have no idea what they are), or, the category theory stuff.
but anyway, so i was reading Wikipedia on category theory. Category theory
in other math articles, say, holomorphic function, homotopy, hilbert space, riemann sphere, homomorphism, etc i've recently read, there's a cold definition. Most of the time, i can at least understand the definition, and go on from there. (in the above examples, i also appreciate what they mean, why they are there, etc, except hilbert space.)
But the category theory, it begin with pages of pages of meta description. And am at loss. But perhaps, to appreciate it, one must first have solid understanding of various branches graduate level math?
but then, my first exposure to it is
Conceptual Mathematics: A First Introduction to Categories by F William Lawvere, Stephen Hoel Schanuel. [Buy at amazon]
in 1990s. Which claimed to be written for laymen, and useful even outside of math. I recall, after reading 1 chapter, it's going too slow, and i was feeling, “what's the point?”. I never continued after the 1 chapter. (i don't have the book now. must gave away or something long ago.)
Math, Naturalness of a Field's Conditions
So, in algebra, you have a field. It's a set and 2 functions f and g, of the form f(a,b) and g(a,b), and X nesting properties of f and g (called commutativity, associativity, distributive, invertible, etc).
So, what happens if we have more than 2 functions, 3 parameters each? So, such study is called universal algebra. (i haven't studied, but i wonder what happens there, in general. The mix of nesting of function, i gather, would create more complex concept similar to associativity and distributive, involving 3 functions, but we don't have a name.)
But, WHAT is the fundamental nature, that real number (a field) is this specific X nesting properties? What is it, that real numbers, which we consider as naturally occurring or developed, form this “field” with such specific nesting properties?
am thinking, there must be some logical answer.
to describe my questions further, for example, real number developed because, first we have counting, 1, 2, 3, then naturally we developed 0, then we have rational, which is ratio, e.g. 1/2 as cutting a pie, then we have negative numbers (from, say, I OWE YOU). And from rational we discovered irrational, as in pythagorean. So there, we have real numbers. And, addition came from simple counting. Multiplication can be considered as a short for repeated additions.
so, am guessing, addition, and multiplication (repeated addition) necessitates the commutativity, associativity, distributive, properties?
now, having written this out, it seems obvious and is the answer to my own question.
... because, by looking at the definition of field, i've always thought, it's somehow arbitrary and complicated. I'd be interested, in a systematic approach of studying structures, e.g. a set, with n operation of m-arity, starting with n=1 and m=1. Then, we develop, all possible ways of nesting n such functions of m arity, so that associativity, commutativity (order of arg), distributivity, are just 3 of the possible properties.
but i gather that, universal algebra may began like this, but actually has become a bit something else.
similar situation is group theory
Group, is much simpler than field. But if you look at definition of group, you see that, it seems also arbitrary and complex.
But then, if you look at symmetry, such as symmetry of polyhedra, you see that all the requirement of group is necessary, and no more, no less.
but the question remain, why is the group definition seems arbitrary?
i mean, is there some point of view, so the associativity
(a • b) • c = a • (b • c)
requirement, dissolved as if it is natural?
again, i really like to see, a combinatorial exploration of all such possible condition of n functions of m arity. (as in universal algebra)
perhaps after seeing that, then one can judge, comparatively, whether the associativity condition is natural.
now, to be sure, function with 1 or 2 arity is actually perhaps the most natural. And 1 or 2 functions is also pretty bare. As opposed to, a structure with function that has 3 arity, or more than 2 functions.
If you just have 1 function, or just function wit 1 arity, than it may become too simple to have interesting things going on.
but again, would like to see a systematic combinatorial list of the conditions that may arise of n functions and m arity.
comment at
https://plus.google.com/+XahLee/posts/6tiAGpLiQ5z
major issues of writing 2D math plotter
when writing 2D math plotter, major issues are
- (1) adoptive sampling. Else, you get kinks at sharp turns.
- (2) divide by zero or ∞. e.g. plot 1/x.
- (3) asymptotes. e.g. in hyperbola
- (4) auto canvas range. (find max/min and/or find point cluster)
Chinese number names
- 10^52 恒河沙 (sands of eternal river)
- 10^56 阿僧祇 (asamkhya)
- 10^60 那由他 (let it go)
- 10^64 不可思議 (unfathomable)
- 10^68 無量大數 (unmeasurable big number)
Quality Free and Legal Math Textbooks https://www.patreon.com/posts/17392806
added a number theory book.
ideal of ring theory
For an arbitrary ring ( R , + , ⋅ ), let (R,+) be its additive group.
A subset I is called a two-sided ideal (or simply an ideal) of R if it is an additive subgroup of R that “absorbs multiplication by elements of R.”
i.e.
- (I,+) is a subgroup of ( R , + )
- ∀ x ∈ I , ∀ r ∈ R : x ⋅ r , r ⋅ x ∈ I
digging out my 3 Volumes classic Mathematical Thought From Ancient to Modern Times Buy at amazon . I haven't read for 20 years. To read about how sin exp were extended to complex plane.
See also: Math and Geometry Books
origami simulator
Origami Simulator, by Amanda Ghassaei, at http://www.amandaghassaei.com/projects/origami_simulator/
added more logic book. Free Math Textbooks
The sound of space-filling curves: examples
this is incredibly beautiful, not just the novelty, but MUSICALLY!
- The sound of space-filling curves: examples
- By Herman Haverkort.
- http://www.win.tue.nl/~hermanh/doku.php?id=sound_of_space-filling_curves
listen to the first one, the hilbert curve (the one “without intro”)
that's the best one. The other ones are not so good.
The author, Herman Haverkort, is a mathematician specializing on algorithms.
Free Math Textbooks (added books on logic)
 Why Are Textbook So Expensive?
Why Are Textbook So Expensive? Escher Chameleon Polyhedron
Escher Chameleon Polyhedron Math and Geometry Books
Math and Geometry Books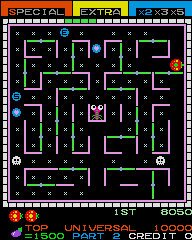 Ladybug Video Game, Optimal Strategy
Ladybug Video Game, Optimal Strategy Polyhedra Chocolate
Polyhedra Chocolate linear algebra anime
linear algebra anime Knit Brain Hat
Knit Brain Hat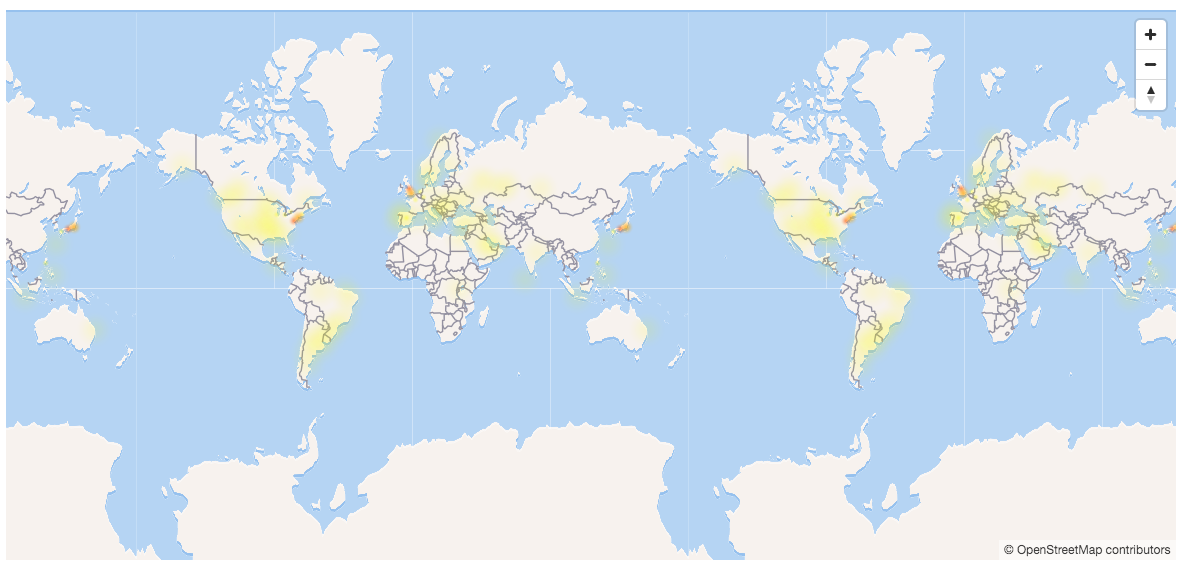 Toroidal Earth Map
Toroidal Earth Map