Xah Math Blog Archive 2011-01
update, with video: Mathematician Grigori Perelman, Million Dollar Prize (2010)
minor updated. Buy the book: “Curves And Their Properties” by Robert Yates
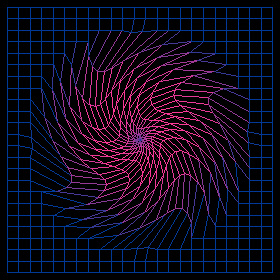
updated. Geometry: Transformation of the Plane
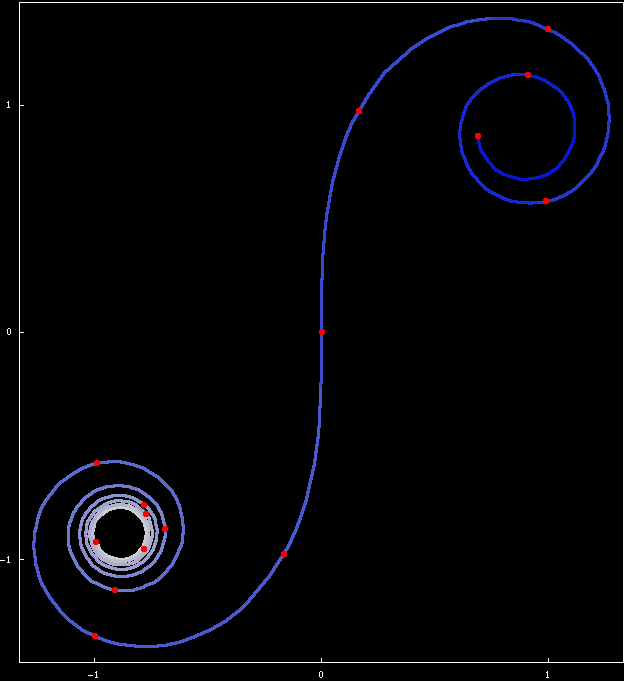
slight update Cornu Spiral .
Math Font, Unicode, Gothic Letters, Double Struck, 𝔄 𝔅 ℭ
Why Does π Occur All Over Math?
for example, just about every interesting plain curve involves π. See: Visual Dictionary of Special Plane Curves .
the only reason i can think of is that it's the circular function. (that is, the essence of trig function. 〔see Sine Curve〕)
but it happens in probability too. For example: Buffon's needle .
the Wikipedia article indicates that Buffon's needle is part of a problem in geometric probability. So, perhaps that ties to the circle, therefore π. Circle itself can be considered as a result of circular function. i.e. the trace of a constant length with one end fixed and the other end moves at a constant speed. So, we can consider that the relation of Buffon's Needle is tied to circular function.
but are there other occurrence of π that has little to do with circle? (For example, it appears in series often. How's this explained?)
Conway's Game of Life Recursively Defined

Russell Towle Died (1949 to 2008)
Xah Lee Introduces Stanford University Courses
Review of Khan Academy by Xah Lee (2011)
Allograph, Variant of the Letter s = ſ and Integral Sign ∫
ID String Length Design, Radix vs Length
Math: Fibonaci Sequence Video Fallacy 📺

This appeared in a perfume video ad: Midnight Poison; Space Dementia; Eva Green .
Math, Sleeves and Xah in Second Life
Thanks to Stanley Rabinowitz of mathpropress.com for donation, for the Visual Dictionary of Special Plane Curves project.
Note that you can purchase the entire project as downloadable file for easy reading on your computer or iPad. See: Buy A Visual Dictionary of Special Plane Curves. I still don't have Mathematica files updated yet, but you'll get free update when available.
Updated my Mathematica package for plotting Geometric Transformation and Complex Function.
Get it at: Wolfram: Transform2DPlot Package 📦
Geometry: Ellipses, Linkages, Solids of Constant Width 📺
Discovered a Unicode math symbol that's from Mathematica: “⧴” (RULE-DELAYED). Are there others? (see: Math Symbols in Unicode.)
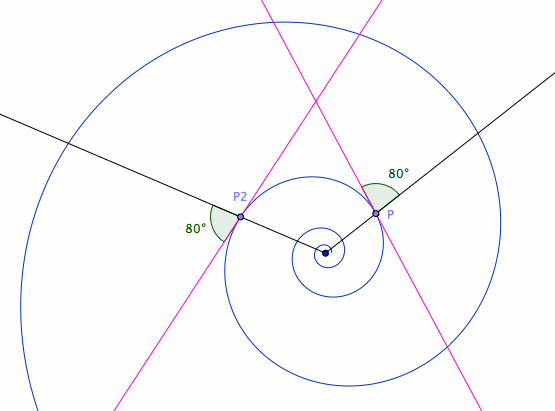
- Update: interactive GeoGebra applet showing Product of Rotations
- GeoGebra: Product of Rotations
Fixed the java certificate problem. Now it works in all browsers: 60+ GeoGebra Files for Plane Curves .
60+ interactive geometry GeoGebra apps for Plane Curves at: Plane Curves: GeoGebra Files Index .
Reminder. If you like this blog, you might also enjoy my other programer related blogs:
- Xah Programing Blog, subscribe here
- Xah Emacs Blog, subscribe here
- Xah Web Dev Blog, subscribe here
- Xah Math Blog, subscribe here
Usually i don't repeat a article in more than one place, even if it's related to both.
Xah's edu corner: How Long is One Year?
There's a extremely simple, nice, web site for creating math notations then you can point a URL to. You type LaTeX code, it displays the results as a image on-the-fly immediately as you edit. It also comes with a short perm URL that you can point to. You can come back to the URL later and edit the expression anytime. The site is at mathurl.com
added to: Tools to Display Math on Web .
Mandelbrot Set Explained (no complex number needed) (with youtube video)
Google made a fractal application, based on Google Maps, at juliamap.googlelabs.com .
Though, am rather disappointed. When you zoom in just a few steps, the resolution does not automatically increase enough to get crispy edges.
Much better are some dedicated fractal apps. See: Great Fractal Software.
For a basic explanation of the mandelbrot set, see: Mandelbrot Set Explained (no complex number needed) .
Looks like a great out of print book Tiling and Patterns By Branko Grunbaüm and G C Shaphard, is being republished by Dover. Buy at amazon
I'd say this is best math book i've ever read. (technically, i'd put this book in one of the top 10 i've read, because there are quite a lot good math books on various topics and written with different style for different audiences.)
below is some very old articles i wrote, about the book and other math books.
I worked intensively on tilings for about a year in around ~1997. The most mathematical is: The Discontinuous Groups of Rotation and Translation in the Plane, which are linked a lot. It is basically my own learning notes. All images are generated by Mathematica, a package i wrote: Plane Tiling Mathematica Package. I'll be updating it from Mathematica v3 to v7 in next few days. At the time, i wanted to create a most versatile software that generates any type of tilings, decorative patterns, without human intervention. A sort of AI in the spirit of Douglas Hofstadter. (See: Gödel, Escher, Bach Buy at amazon) Of course, i didn't get that far. For gallery, see: Math Tiling and Patterns Gallery.
All these pages are written in late 1990s. Much update needs to be done, on the html and the writing too.
combinatorics and space-filling curves
Robert Dickau has done many nice combinatorial diagrams with Mathematica. For example, here's some i like:
- Bell Numbers @ http://robertdickau.com/bell.html
- All Self-Avoiding Paths Through a Lattice @ http://robertdickau.com/allpaths.html
- Stamp Folding @ http://robertdickau.com/stampfolding.html
His home page robertdickau.com has many more. You can also get many of his interactive Mathematica files at demonstrations.wolfram.com .
You might also enjoy a combinatorics diagram i did. See: Number Of Ways To Loop n Points. (it was done with Mathematica v3. I'll update the notebook to v7 soon.)
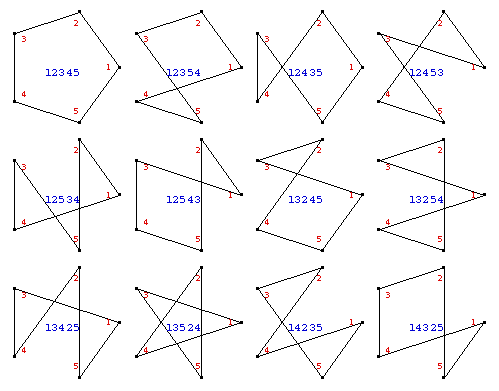
Many of Robert's work are about space filling curves. It is one of the math i learned in early 1990s that had a big effect on me. In short, it shows that there are same number of points of one side of a square to the square itself. At the time, it was a shock to mathematicians. See: Space-filling curve, and Xah's Top 10 Math Wonders .
3D Visualization Design (wolfram demo project; commentary; tips)
 Magic Polyhedrons
Magic Polyhedrons Bejeweled Blitz Strategy as Math
Bejeweled Blitz Strategy as Math Math Mysticism: is Hurricane Shape a Fibonaci Spiral?
Math Mysticism: is Hurricane Shape a Fibonaci Spiral?