Xah Math Blog Archive 2013-01
The Geometric Significance of Complex Conjugate (oldie but goodie)
Vectors and Complex Numbers
complex numbers, or complex analysis, is one of the most beautiful math. If you don't know complex numbers, and you love geometry, it is essential you get to know it.
updated:
Stereographic Projection 3D-Printed Physical Model
Astroid as Catacaustic of Deltoid
yay, my site made it to AMS blog.
- Astroid as Catacaustic of Deltoid
- By John Baez.
- http://blogs.ams.org/visualinsight/2013/11/15/astroid-as-catacaustic-of-deltoid/
it's written by the redoubtable mathematician [John Baez https://plus.google.com/117663015413546257905/posts]. Baez is great, in that he writes serious math for any math undergraduate to appreciate, as opposed to many math popularizing authors who write for the laymen.
i did my curves project Visual Dictionary of Special Plane Curves mostly in 1994 to 1997, almost 2 decades ago, while i was a college student. I never seen the proof of how Deltoid's Catacaustic is a Astroid. I recall trying to, but it was too difficult for me back then. I haven't done much math since.
Do you know a proof of how Deltoid's Catacaustic is a Astroid? Post to [John's Google Plus post https://plus.google.com/u/0/117663015413546257905/posts/BHTQX8tfiaV]. Thanks.
Equiangular Spiral, also known as log spiral, has the property that the angle of tangent to center is constant.
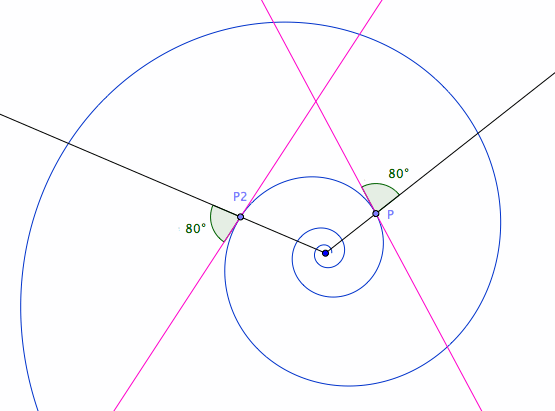
Mathematician Jacob Bernoulli (1654 to 1705) requested this spiral be engraved on his tombstone with the epitaph:
Though changed I rise unchanged
more pics and properties at Equiangular Spiral
have you ever heard people say “i am never good at math…”?
hi, am a mathematician. When the subject of math comes up in conversation, the usual response i get is a somewhat uneasy utterance of “i am never good at math”.
you know what? that's right, you are a idiot, period.
FACT OF LIFE❗
Math Terminology: Magma vs Groupoid
The term magma for this kind of structure was introduced by Nicolas Bourbaki. The term groupoid is an older, but still commonly used alternative which was introduced by Øystein Ore.
why did the Bourbaki guys introduce the term magma? it seems to me groupoid is a better term. Was it introduced to avoid confusion due to the many slightly different definitions of groupoid?
Why is Sine Called Circular Function
this is why sine, cosine, are called circular functions
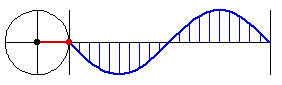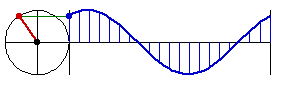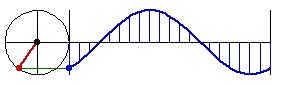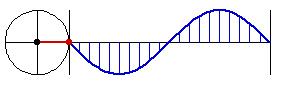
all the trig function, {sin, cos, tan, asin, acos, atan}, can be defined using just one of them, sin.
so, there is really just one function: sine.
you can see why it's so important in math, because the nature of it is that it's the height when you sweep a circle with constant speed.
in other words, anything that rotates in a constant speed, sine is in it.
earth rotates, moon rotates, so came sine. Then, wheels are invented, more sine.
read more at Sine Curve
math gothic font. Can you identify the following letters? 𝔅 𝔙
On the Naming of Eigenvector and the Igon Value Problem
the Nature of Linear Transformation
math demystification: If you hear “stochastic process”, you can safely replace it with “random process”
The gist here is to distill a math art into its algorithmic essence. By recursion or some encoding (such as math equation)
my concern in life is math and women. But since they are both difficult, my activity is mostly reduced to visualization aspect.
What is Riemann Surface? Understanding the Concept Without Math.
Wikipedia Reading Snippets: Understanding Category Theory
In many fields of mathematics, morphism refers to a structure-preserving mapping from one mathematical structure to another. The notion of morphism recurs in much of contemporary mathematics. In set theory, morphisms are functions; in linear algebra, linear transformations; in group theory, group homomorphisms; in topology, continuous functions, and so on.
In category theory, morphism is a broadly similar idea, but somewhat more abstract: the mathematical objects involved need not be sets, and the relationship between them may be something more general than a map.
The study of morphisms and of the structures (called objects) over which they are defined, is central to category theory. Much of the terminology of morphisms, as well as the intuition underlying them, comes from concrete categories, where the objects are simply sets with some additional structure, and morphisms are structure-preserving functions. In category theory, morphisms are sometimes also called arrows.
Quality of Terminology In Computer Languages (2008)
Math Writing Style: Use of the Term “Linear Operator” vs “Linear Function”
What is Quadratic Form in Math?
homeomorphism, and homotopy for 1/z
“homeomorphism” (aka “topological isomorphism”, “bicontinuous function”) is a continuous function between topological spaces that has a continuous inverse function.
In topology, two continuous functions from one topological space to another are called homotopic if one can be “continuously deformed” into the other, such a deformation being called a homotopy between the two functions.
is there a homotopy that maps identity in the complex plane to 1/conjugate[z]? or sin[z]?

i think there is. It's obvious, that if the 2 spaces are topologically equivalent, there always is, the question is to find the homotopy. In my case, just use the idea of Geometric Inversion. Let p be the point in domain and p' in range, then just smoothly swap them by gradually narrowing their distance.
Mathematician: Yitang Zhang, Twin Prime Conjecture Breakthru
updated
The Significance of Complex Numbers: Frobenius Theorem
the Nature of Associative Property of Algebra
the meaning of the word variety is varied. There's variety show, then there's algebraic variety. The variegation and etymology is fantastic, not to mention manifold.
show your calculator to Euler and Gauss. Best Graphing Calculator
(old. Added YouTube videos)
The TeX Pestilence: Why TeX LaTeX Sucks (2004) (updated)
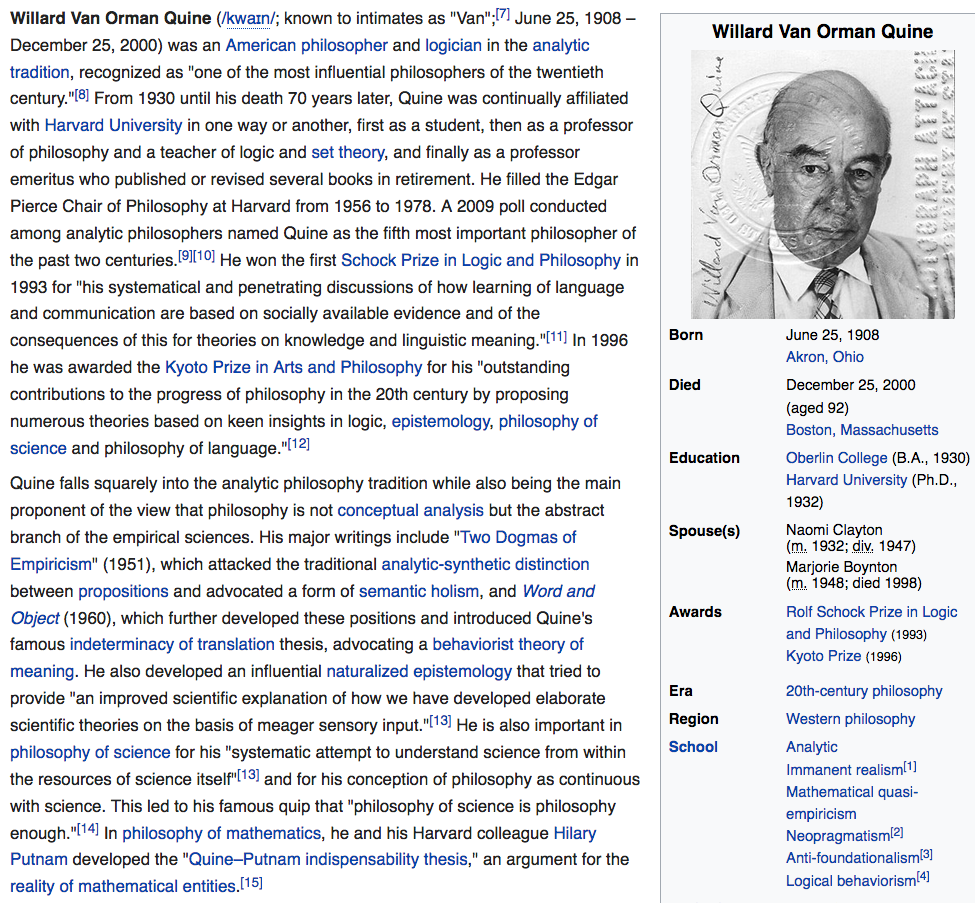
one of my hero. Willard Van Orman Quine (1908 to 2000). A logical positivists, a logician.
logic and linguistics. The Logical Levels of Interpretation
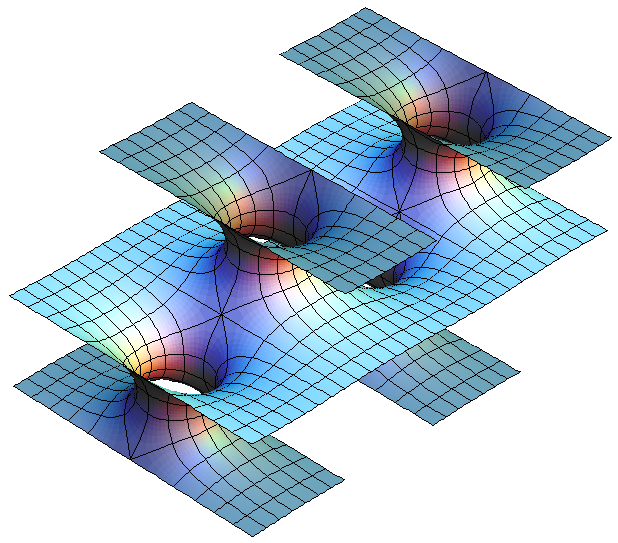
Dead Reckoning in a Non-Orientable 3D Space
Geometric Dissection, Mechanical Iris, Expandable Table Furniture 📺 (updated)
GeoGebra No Longer FSF Free Software
GeoGebra was open source (GPL) for about 10 years (up to version 4.0), but since version 4.2, now only for non-commercial use. This is bate and switch, but the problem is really open source. When it gets big, it needs funding, but nobody wants to pay.
Here is quote from Wikipedia GeoGebra on its licensing:
Most parts of the GeoGebra program are licensed under GPL, making them free software. However some parts, including the Windows and Mac installers, have a license which forbids commercial use and are therefore not free software.[9][10][11] In practice, this means that non-commercial use by teachers and students is always free of charge, while commercial users may need to pay license fees. For details see the GeoGebra license description.[9]
Since July 2010 the Debian GNU/Linux distribution offers a free version of GeoGebra 4.0 in which all un-free parts of the program were removed or replaced by free software. This version may be used for commercial purposes without paying licensing fees. However, starting with version 4.2 since December 2012, the license is changed to be more restrictive[11] so that GeoGebra cannot be included in Debian GNU/Linux any longer. On the other hand, the software can still be downloaded from its official download page free of charge for many platforms (including Debian as well).
GeoGebra is a Java Applet. But since Apple Apple killed Flash in 2010, as well as not including Java, Java applet is pretty much dead (it doesn't run on any Apple iOS nor Google Android phone/tablet).
GeoGebra just came up with a tablet version from a KickStarter project that got funding of $12k from 310 backers. 〔http://www.kickstarter.com/projects/geogebra/geogebra-for-the-ipad/posts/488589〕.
60 Plane Curves GeoGebra Files
Projective Geometry Java Applets
Some old projective geometry interactive applets. Requires Java installed.
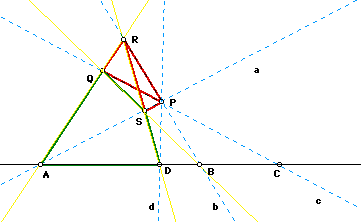
The main file is Intro to Real Projective Plane
following are Java applets.
../projective_geometry/z/_z_17_quadrangle_2.4a.html../projective_geometry/z/_z_17_quadrangleConst_2.42.html../projective_geometry/z/_z_17_quadrilateral_2.4b.html../projective_geometry/z/_z_desarguesTheorem.html../projective_geometry/z/_z_harmonic_points_const.html../projective_geometry/z/_z_harmonic_points.html../projective_geometry/z/_z_perspTriangles.html
Rewriting them in JavaScript soon.
A great blog from a architect. Always lots of most beautiful math images. Be sure to checkout his past articles.
- eat-a-bug: Art, Design, Architecture, and Technology
- By Lorenz Lachauer.
- http://eat-a-bug.blogspot.com/
JavaScript D3 Rotating Voronoi Demo
Sum of Angles of Triangle on Girl's Chest (math humor)
compass and straightedge in JavaScript. Try it. http://sciencevsmagic.net/geo/
for many other similar software, see Great Software for Plane Geometry
Math: Symmetry, Flatland, by Ian Stewart
A new book.
- Symmetry: A Very Short Introduction
- By Ian Stewart.
- Buy at amazon
It cited my work: Discontinuous Groups of Rotation and Translation in the Plane. ☺
Ian Stewart is a well-known mathematician. He has written many books introducing interesting math to the laymen. Including:
- Flatterland: Like Flatland, Only More So
- By Ian Stewart.
- Buy at amazon
- The Annotated Flatland: A Romance of Many Dimensions
- By Ian Stewart.
- Buy at amazon
You can also read Flatland here: FLATLAND: A Romance of Many Dimensions
There's also a Chinese translation: 神奇的二维国 (Flatland)
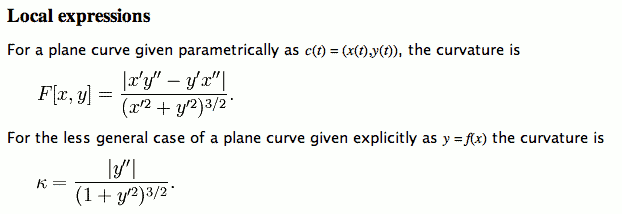
The Problems of Traditional Math Notation
now, you can use this search box: Unicode Search 🔎 to find all your math symbols.

see also: Teacup Recursion Animation
a project by a old friend at Wolfram Research. 〈The State of the Unit: The Kilogram〉 http://www.kickstarter.com/projects/52746223/the-state-of-the-unit-the-kilogram-documentary-fil?ref=live
read this, and you'll understand everything about complex numbers, without hearing a word of “complex”. Coordinate Transformation
Math Symbols in Unicode. Now, hover your mouse over to see the full symbol name.
a blog by Glenn Wilcox with lots beautiful math-related pictures generated in Rhinoceros 3D At http://www.generativedesigncomputing.net/
O, math, my true love, but how i have alienated thee, and you being quite difficult.
Microwave Arithmetic
on a microwave, you press 2 0 0 for 120 seconds, but 1 2 0 for 80 seconds, yet 9 0 for 90 seconds.
can you establish the rules for microwave number system or microwave arithmetic?
recursion bonanza: Teacup Recursion Animation
5-Point Conics (needs Java installed.)
Logic Based Human Language: Lojban
Lojban is a constructed language, design based on predicate logic. Some tutorial here, with voice recording.
Alice in Wonderland, Zero-sum game
“The more there is of mine, the less there is of yours.”
That's the concept of Zero-sum game. However, in real world, most things isn't zero-sum game. Both parties actually benefit. For example, when you give something you no longer want to someone, a value is created “out of nothing”.
 Go Board Game on Hexagonal and Triangular Grids
Go Board Game on Hexagonal and Triangular Grids Algorithmic Mathematical Art
Algorithmic Mathematical Art Space-Filling Curve
Space-Filling Curve The Geometric Significance of Complex Conjugate
The Geometric Significance of Complex Conjugate Understanding Complex Numbers
Understanding Complex Numbers Beauty of Roots
Beauty of Roots Maze and Math in Video Games
Maze and Math in Video Games Tools to Display Math on Web
Tools to Display Math on Web Polyhedra Chocolate
Polyhedra Chocolate Visual Illusions
Visual Illusions linear algebra anime
linear algebra anime Doyle Spiral and Mobius Transformation
Doyle Spiral and Mobius Transformation