Xah Math Blog Archive 2015-01
- What Is Spacetime, Really?
- By Stephen Wolfram.
- http://blog.stephenwolfram.com/2015/12/what-is-spacetime-really/
see also
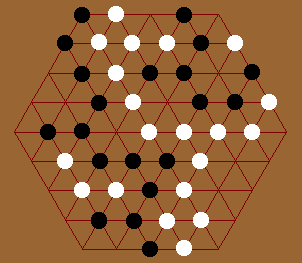
Numbering System of Hex Grids
Comprehensive Hexagonal Grids programing tutorial. added to
http://modto.com/integral-house-by-shim-sutcliffe-architects/
- Berkeley to fire 'love letter to learning' professor
- By Rory Carroll.
- http://www.theguardian.com/us-news/2015/oct/17/berkeley-math-professor-alexander-coward-campus-battle
- BLOWING THE WHISTLE ON THE UC BERKELEY MATHEMATICS DEPARTMENT
- By Alexander Coward.
- http://alexandercoward.com/BlowingTheWhistleOnUCBerkeleyMathematics.html
ancient article, still relevant. Google Chrome killed MathML. The TeX Pestilence: Why TeX LaTeX Sucks
Math and Geometry Booksthe Nature of Associative Property of Algebra (minor update)
- The reason why Involute gears turn smoothly.
- By Hyprodium.
- http://hyrodium.tumblr.com/post/123270340099/the-reason-why-involute-gears-turn-smoothly-fig
see also Involute
- John Horton Conway: the world's most charismatic mathematician
- By Siobhan Roberts.
- http://www.theguardian.com/science/2015/jul/23/john-horton-conway-the-most-charismatic-mathematician-in-the-world
Abacusa new book. A biography of John Horton Conway
- Genius At Play: The Curious Mind of John Horton Conway
- By Siobhan Roberts.
- Buy at amazon
Chen's theorem: every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes). Chen's theorem
〔A Guide to Plane Algebraic Curves by Keith Kending. At Buy at amazon〕
The Stanford Encyclopedia of Philosophy
The Stanford Encyclopedia of Philosophy is a great thing. A different take than Wikipedia.
magic polyhedron
the Rubik cube of today have advanced. Now, there's stickerless versions, and better mechanical design.
Magic Polyhedronsℭ = Cardinality of the continuum.
ℚ = be rational, ℝ = get real.
ℭ = Cardinality of the continuum.
Tiling and Patterns, Classic Text Now in Print Again
just discovered, this classic, definitive, book on tilings and patterns is in print again, now reprinted by Dover.
Reading Notes on Tilings and Patternstiling the plane with 5-fold symmetry tiles
John Baez, gave a intro on the problem of tiling the plane with 5-fold symmetry tiles At https://plus.google.com/117663015413546257905/posts/5CHdeLRckRm
see also
- The trouble with five
- By Craig Kaplan.
- https://plus.maths.org/content/trouble-five
sample of tiling and patterns, see:
See also: Discontinuous Groups of Rotation and Translation in the Plane
Skew Dice But FairCycloid (animation update)
Unicode Char for Logarithm?
apparently there's a Unicode char for log. ㏒. The Unicode name is “U+33D2: SQUARE LOG”. It's Japanese origin.
There's also a ㏑ “U+33D1: SQUARE LN”
for many more, see http://www.unicode.org/charts/PDF/U3300.pdf
See also: Unicode: Math Symbols π² ∞ ∫
(thanks to https://x.com/Ryuutei)
English/Chinese Math Terminology 中/英 数学术语 (minor update)
LimaconOfPascal (updated gif animation)
Trochoid (updated gif animation)
Tractrix (updated gif animation)
Conchoid (minor update)
Notes on A New Kind of Science (Cellular Automata, Computation Systems) (photo of the book added)
How to Lose Interest at Go Board Game Fast
in early 1990s i spend 2 years playing go. At the time i bought the best go program called Nemesis for the Mac. Was able to beat it with 5 stone handicap for the computer. (the software is rated 13 kyu, which means, i'm i think 9kyu at the time)
some said that playing with computers gets you bad habits…
sometimes in 2009 or so, i suddenly find go to be not interesting at all, after i read Stephen Wolfram's “A New Kind of Science”.
the essence is that it's a kinda a cellular automata, and as such, there is no intrinsic math in it, and there are infinite cellular automata. And go players are simply those with great memory and specialized talent and seen lots of cellular automata of the go kind…
see Go Board Game as Cellular Automata
the other thing that has been interesting for me to explore is go on triangular grid or other tiling. Though, it's disappointing that i haven't seen much literature about it at all.
how to lose all interest in go. Go Board Game as Cellular Automata
What is Technical Drawing, Descriptive Geometry, Projective Geometry, Linear Algebra (minor update)
Extending the Euclidean Plane: Riemann Sphere and Real Projective Plane
Unicode: Math Symbols π² ∞ ∫ (minor update)
Visual Complex Functions by Elias Wegert. Buy at amazon
Schmidt Arrangement, Algebra Integer, Gaussian integer, Eisenstein Integer
Stereographic Projection and Geometric Inversion
Stereographic projection is a special case of sphere inversion.
consider a sphere of diameter d, and plane at bottom. The inversion circle is centered on North pole, with diameter 2*d.
also:
Stereographic Projection (minor update Mathematica notebook. If you have a problem running it, let me know, i'll fix.)
Table of mathematical symbols by introduction date
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem defined by a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are nonlinear.[1] It is the sub-field of Mathematical optimization that deals with problems that are not linear.