Tractrix

Mathematica Notebook for This Page .

History

From Robert Yates:

Studied by Christiaan Huygens in 1692 and later by Gottfried Leibniz, Johann Bernoulli, Liouvlle, and Eugenio Beltrami. Also called Tractory and Equitangential Curve.

Description

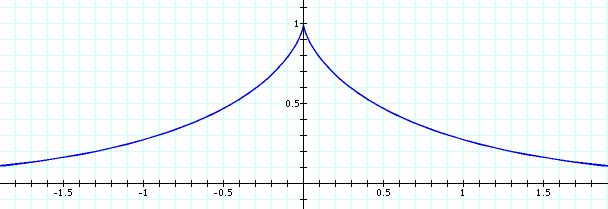
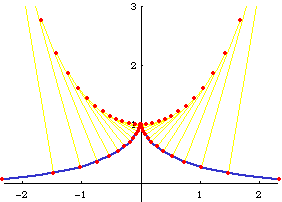
Tracktrix (equitangential curve, tractory) is a curve such that any tangent segment from the tangent point on the curve to the curve's asymptote have constant length.

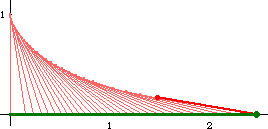
Suppose a bicycle with front wheel at the {0,0} and back wheel at {0,1}. The front wheel is turned to head East. The track traced by the back wheel is the tractrix. Note that the tractrix's asymptote cuts its tangents into segments of equal length.

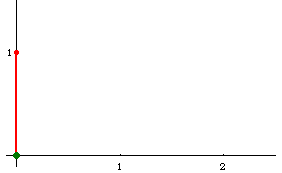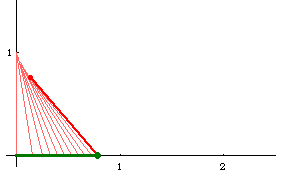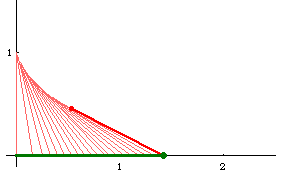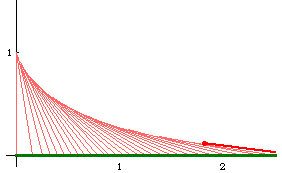
Formula

Parametric: {Log[Sec[t] + Tan[t]] - Sin[t], Cos[t]}, -Pi/2 < t < Pi/2.

Cartesian: x == Log[(1 -Sqrt[1^2-y^2])/y] + Sqrt[1^2-y^2].

Properties

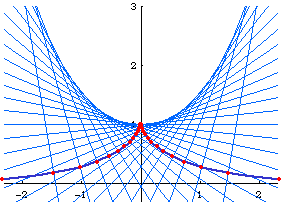
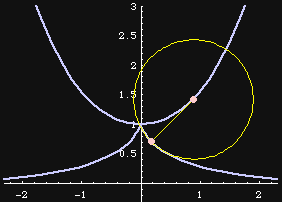
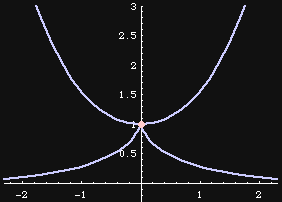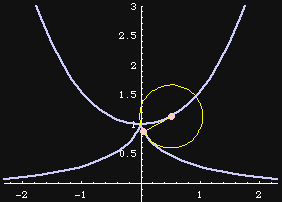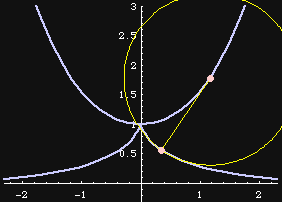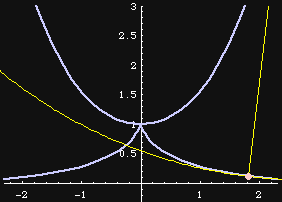
Orthogonal to Circles

The tractrix is orthogonal to a set of circles centered on the tractrix's asymptote, all having radius radius R. R is the same as the tractrix's constant length tangent segment.

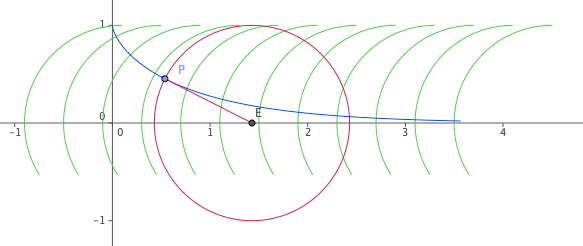
Tractrix and Catenary

The evolute of tractrix is catenary, conversely, the involute of catenary is tractrix.

Pseudosphere

The surface of revolution of tractrix around its asymptote is called pseudosphere. Eugenio Beltrami in 1868 showed that pseudosphere provided a model for hyperbolic geometry. It is a surface of constant negative Gaussian curvature.

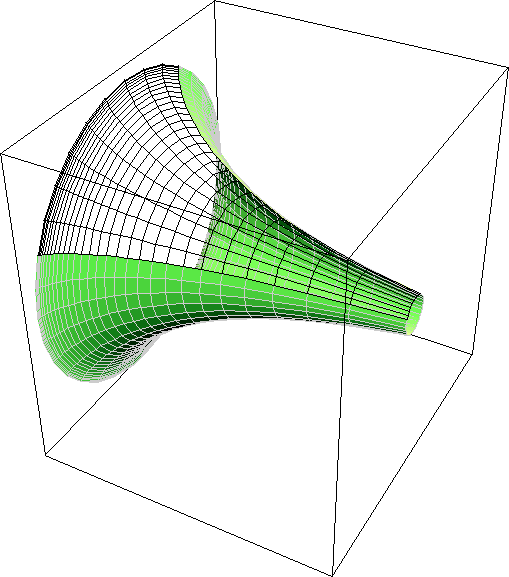
See also: pseudosphere .

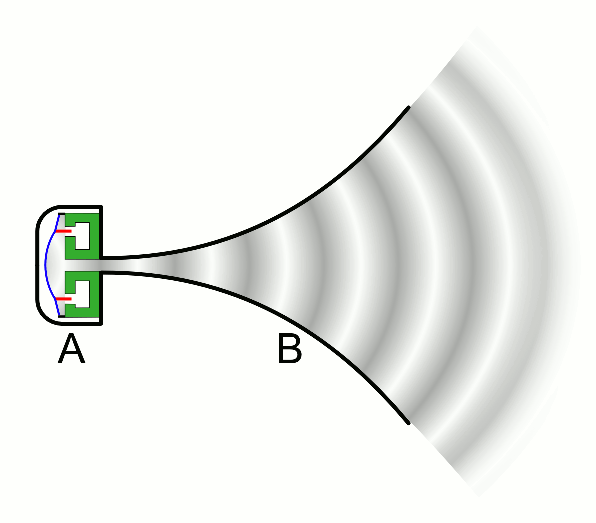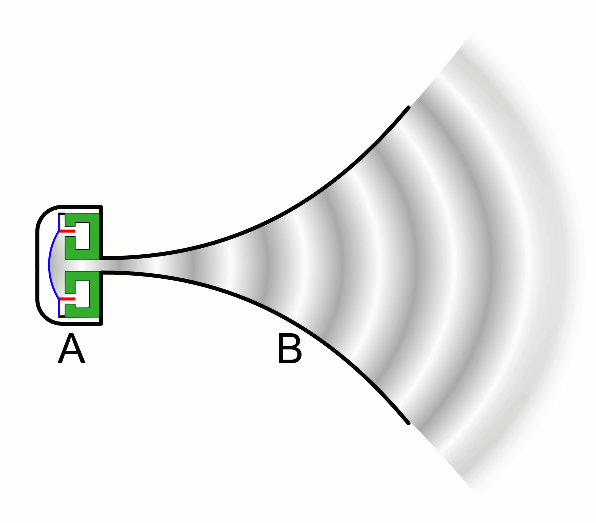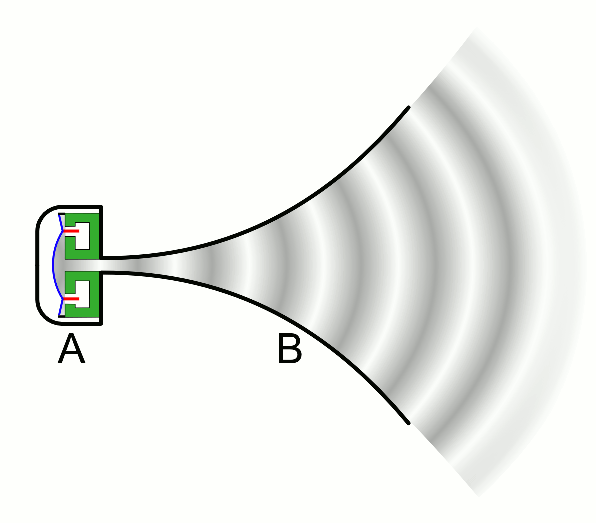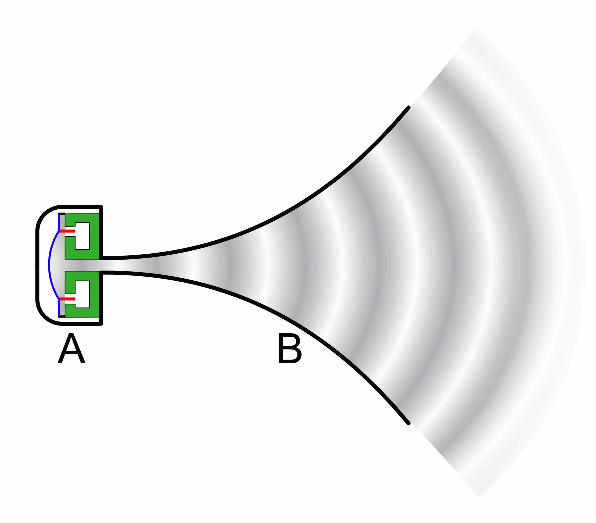
Applications

The tractrix is a ideal shape for a horn loudspeaker.

Related Web Sites

See: Websites on Plane Curves, Plane Curves Books .

The MacTutor History of Mathematics archive

Robert Yates: Curves and Their Properties .