Conchoid
Mathematica Notebook for This Page .
History
A generalization of methods of conchoid of Nicomedes, invented by Nicomedes (~225 BC) to trisect a angle. Who first generalized this? Why?
Description
Conchoid is a way of deriving a new curve based on a given curve, a fixed point, and a positive constant k. Curves generated this way are sometimes called general conchoid because this method is a generalization of conchoid of Nicomedes .
Step-by-step description:
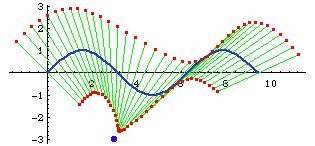
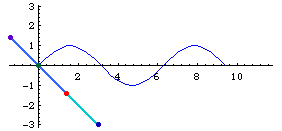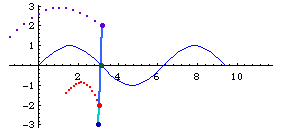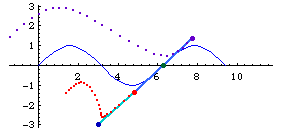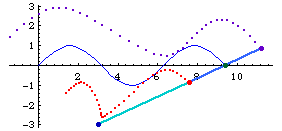
- Given a curve c, a point O not on l, and a constant k.
- Draw a line m passing O and any point P on C.
- Mark points Q1 and Q2 on m such that distance[Q1,P]==distance[Q2,p]==k.
- The locus of Q1 and Q2 for variable points P on c is the conchoid of c with respect to O and offset k.
The point O is called the pole.
Formula
Conchoids has two branches. We associate the +Abs[k] offset to the branch that lies on the side of the given curve opposite the pole, and the -Abs[k] offset corresponds to the branch that lies on the same side as the pole. Often, it is better to define conchoid with a signed offset, so that a conchoid with a signed constant k has just one branch. If we want both branches, we say a conchoid with offsets k and -k. In the following formulas, k is a signed constant.
If a curve is given in polar form r==f[θ], then its conchoid with respect to the pole and offset k is r==f[θ]+k.
The formula for a conchoid of a point {x,y} with pole at {a,b} and offset k in Cartesian coordinate is: {x + (k*(-a + x))/Sqrt[(-a + x)^2 + (-b + y)^2], y + (k*(-b + y))/Sqrt[(-a + x)^2 + (-b + y)^2]}.
The formula can be easily derived using vectors. Suppose V:={x,y} is a vector. We want to find its conchoid point with respect to the origin and offset k. Immediatly, the conchoid points are located in the direction of V with distance (length[V]+k), where k can be both positive or negative. We multiply the unit vector (V/length[V]) by the required length: (V/length[V])*(length[V]+k). This simplifies to V+(k*V)/length[V] or {x,y}*(1+k/Sqrt[x^2+y^2]). If the pole O is at {a,b}, the we can subsitute V by V-O, and translate the whole thing back by adding {a,b}, resulting the general formula.
Properties
Examples
- Conchoid of a line. (See: conchoid of Nicomedes)
- Conchoid of a circle. conchoid of a circle proof or disproof that certain conchoid of circle is a Cartesian oval.
Verbatim from E.H.Littlewoods, 1961:
- The conchoid of a lemniscate with respect to its center, the fixed distance between equal to the distance from the center to the furthest point of the curve.
- The focal conchoids of the conic sections. (In these conchoids the outer branch is of little interest, having roughly the same shape as the original conic; but the inner branch takes various forms according t the magnitude of he fixed distance. Thus, for the parabola, if the distance from the focus to the vertex is a, the form varies according to whether the fixed distance is (i) less than a, (ii) equal to a, (iii) between a and 2*a, (iv) equal to 2*a, or (v) greater than 2*a. For the ellipse, if A'A is the major axis, with C the center and S the focus nearer to A, and SL the semi-latus-rectum, the two principal forms occur (i) when the fixed distance is between SA and SL, or between CA and SA', (ii) when it is between SL and CA.)
Related Web Sites
Robert Yates: Curves and Their Properties .