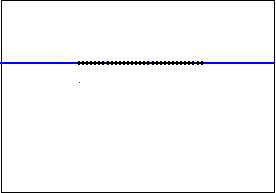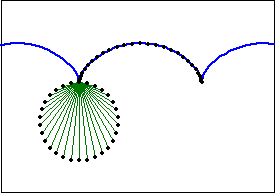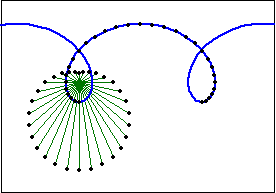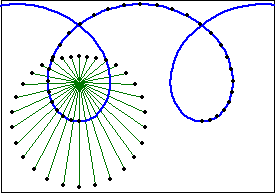Trochoid

Mathematica Notebook for This Page .

History

Description

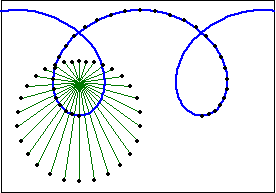
Trochoid describe a family of curves. (See: Curve Family Index) Trochoid is defined as the trace of a point fixed on a circle that rolls along a line. Sometimes the name trochoid is used to mean hypotrochoid and epitrochoid. (curve traced by rolling circle on another circle) More generally, trochoid is any curve that is the locus of a point fixed to a curve A, while A rolls on another curve B without slipping.

Formula

Let the radius of the rolling circle be r and the distance from the tracing point Q to the center of the circle be h.

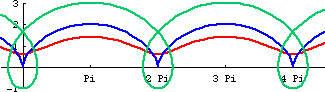
• Parametric: {r t - h Sin[t], r - h Cos[t]}. Periodicy: 2 π.

Properties

Special Cases

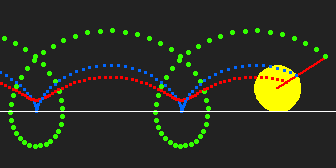
• If Q lies on the rolling circle, it is a cycloid.
• If Q lies outside the rolling circle, it is sometimes called prolate (extended) cycloid.
• If Q lies inside the rolling circle, it is curtate (contracted) cycloid.

Related Web Sites

See: Websites on Plane Curves, Plane Curves Books .

Robert Yates: Curves and Their Properties .