Limacon Of Pascal

Mathematica Notebook for This Page .

History

Discovered and named after Étienne Pascal (1588 to 1651), father of Blaise Pascal (1623 to 1662). Also discussed by Gilles de Roberval (1602 to 1675) in 1650.

… the curve had already been given by Albrecht Dürer (1471 to 1528) in the early sixteenth century.

An Introduction to the History of Math Buy at amazon By Howard Eves, 6th edition, 1989 Problem Studies 4.7, p.128.

Description

Limacon of Pascal describe a family of curves. It is a special case of epitrochoid. (See: Curve Family Index) It can also be defined as a conchoid of a circle. Cardioid and trisectrix are special cases of Limacon of Pascal.

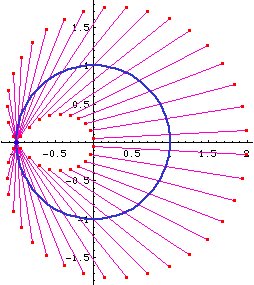
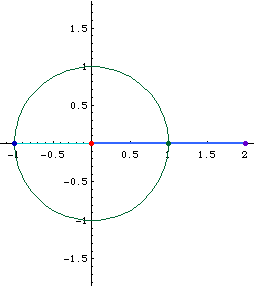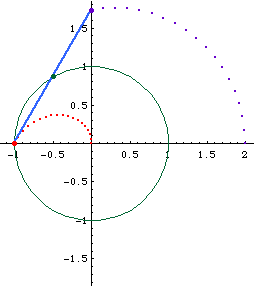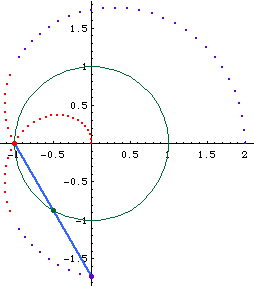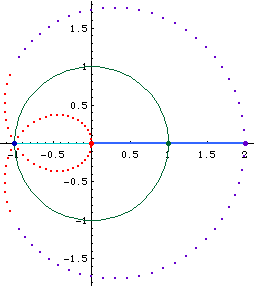
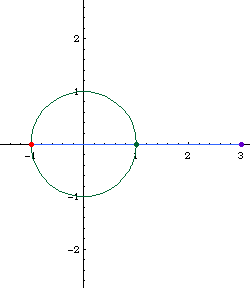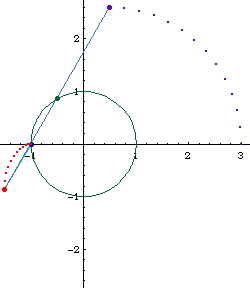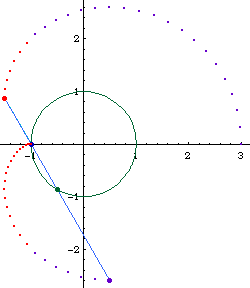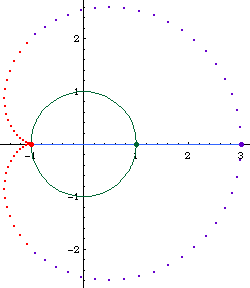
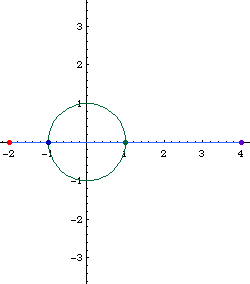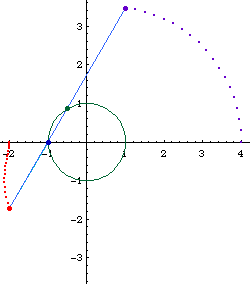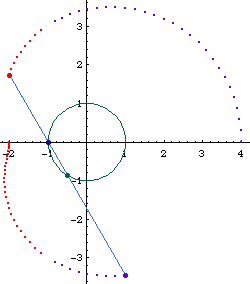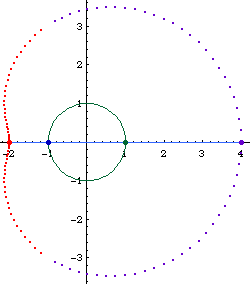
Limacon of Pascal as a conchoid:

1. Let there be a fixed point O on a circle.
2. Draw a line passing O and P, where P is any point on the circle.
3. On this line, mark points Q1 and Q2 such that distance[P,Q1] == distance[P,Q2] == k, where k is a constant.
4. Repeat step 2, 3 for different choice of P. The locus of Q is the Limacon of Pascal.

Formula

• Parametric: (k + 2 r Cos[t]) {Cos[t], Sin[t]}.
• Polar: R == (k + 2 r Cos[t]).
• Cartesian: (x^2 + y^2 -2 r x)^2 == k^2 (x^2 + y^2).

Properties

Special Cases

• if 2 r > k, there is a inner loop.
• if 2 r == k, there is a cusp. (it is a cardioid)
• If 2 r ≤ k, it is a dimpled limacon.
• If r == k, it is the trisectrix

Epitrochoid

Limacon of Pascal is a special case of epitrochoid, when the rolling and fixed circles has equal radius. i.e., it is the trace of a point Q fixed to a circle that rolls around another circle of the same size.

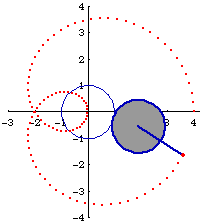
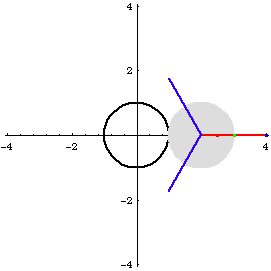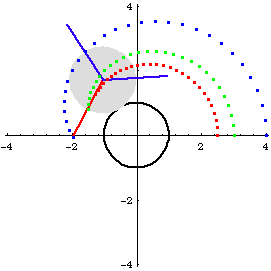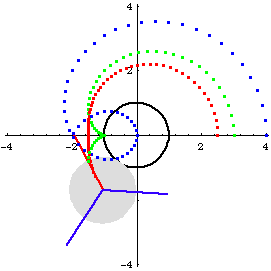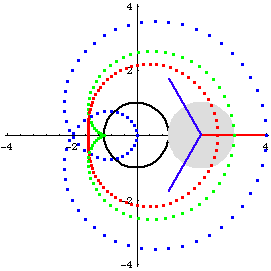
Let radius of circle B and A be r, and Let the distance from the tracing point Q to the center of circle B be h. The parametric formula is then {2 r Cos[t] + h Cos[2 t], 2 r Sin[t] + h Sin[2 t]} with a period of 2 π.

Pedal

Limacon of Pascal is the pedal of a circle with respect to any point in the plane.

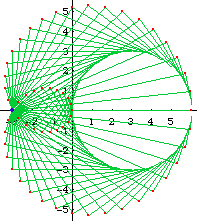
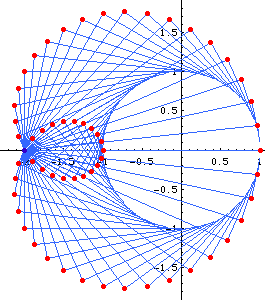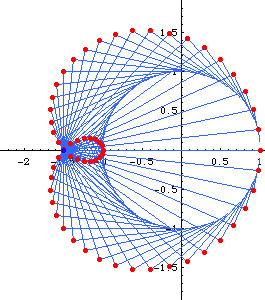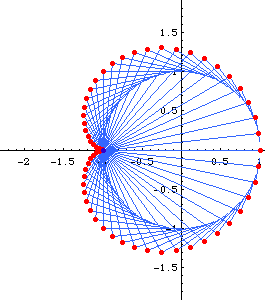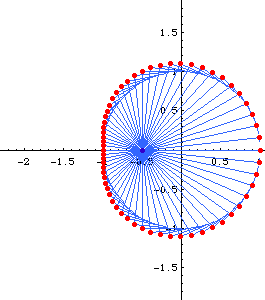
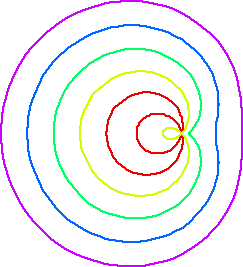
Envelope of Circles

Limacon of Pascal is the envelope of circles with centers on a given circle C and each circle passing through a fixed point P in the plane. (See: limacon of Pascal graphics gallery)

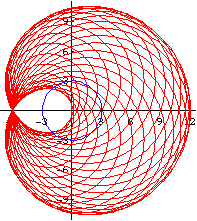
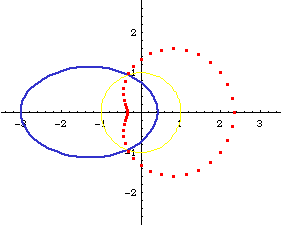
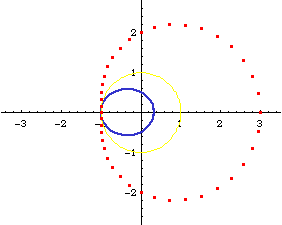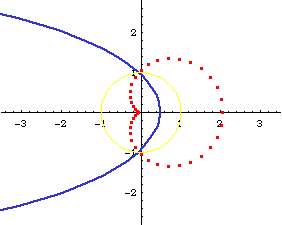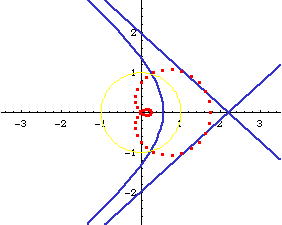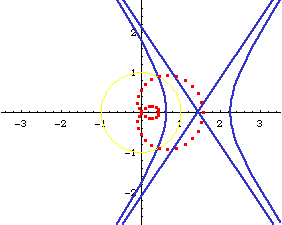
Relation to Conic Sections

Limacon of Pascal is the inversion of conic sections with respect to a focus.

Limacon Graphics Gallery

• Limacon Graphics Gallery

Related Web Sites

See: Websites on Plane Curves, Plane Curves Books .

Robert Yates: Curves and Their Properties .

The MacTutor History of Mathematics archive