Involute

Mathematica Notebook for This Page.

History

Studied by Huygens in 1693.

Description

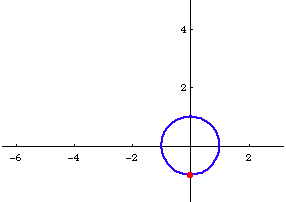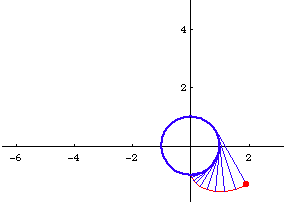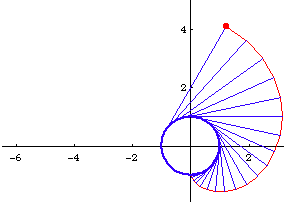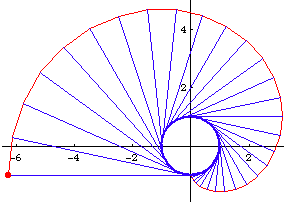
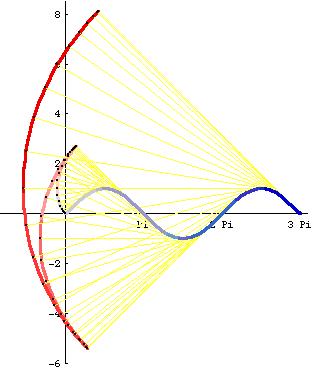
Involute is a general method to generate curves. It is the Roulette of a line. That is, the trace of a point fixed on a line as the line rolls around the given curve.

Step by step description:

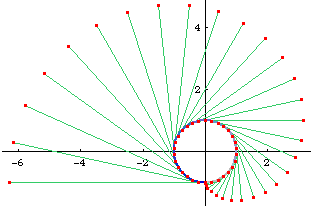
1. Given a curve (a unit circle for example) and a point O on the curve.
2. Imagine a point P on the curve starting from O and moving through the curve.
3. At each moment in time, let there be a tangent at P.
4. Mark a point Q on this tangent such that the arc length from O to P is equal the line length P to Q. (there are two such points, take the one that lies “behind” P)
5. The locus of Q is the involute of the given directioned curve with respect to the point O on the curve.

Formulas

Given a curve in parametric form {xf[t], yf[t]} , its involute starting at t:=t0 is:

{xf[t]- s[t]* xf'[t]/Sqrt[xf'[t]^2+yf'[t]^2],
 yf[t]- s[t]* yf'[t]/Sqrt[xf'[t]^2+yf'[t]^2]}

where s[t] is the arc length function:

s[t]:=Integrate[Sqrt[(xf'[x])^2 + (yf'[x])^2], {x,t0,t}]

The involute formula is easily derived. Take the tangent vector at t, make it unit length (divide by its length), then multiply that by the arc length from t0 to t, negate it, then add the vector at t to translate it back to the location P the curve. If the parametric formula {xf,yf} is denoted using the complex function z[t], z[t]:=xf[t]+I*yf[t], we can write it as:

-(z'[t]/|z'[t]|)*s[t] + z[t]

Properties

Involutes are Parallel

All involutes of a given curve are parallel to each other. This property also makes it easy to see that evolute of a curve is the envelope of its normals.

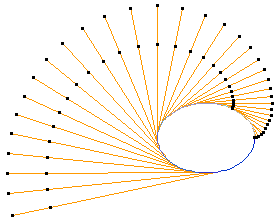
Involute and Evolute

If curve A is the evolute of curve B, then curve B is the involute of curve A. The converse is true locally, that is: If curve B is the involute of curve A, then any part of curve A is the evolute of some parts of B.

Interconnection of Curves

Many special curves share the evolute/involute relationship. See the table at the evolute page.

Related Web Sites

See: Websites on Plane Curves, Printed References On Plane Curves.

Robert Yates: Curves and Their Properties.

involute.

HowStuffWorks.com on Gears. http://www.howstuffworks.com/gear.htm/printable