Cycloid

Mathematica Notebook for This Page .

radial evolute negative pedal pedal caustic parallel inversion derivative cissoid wrt a line conchoid strophoid

History

Description

Cycloid (tautochrone, brachistochrone) is a member of cycloidal family of curves. (See: Curve Family Index) Prolate (extended) or curtate (contracted) cycloids are also known as trochoids. In this page, we use the narrowest definition of the term cycloid, defined as the trace of a point on the circumsference of a circle rolling on a line without slipping.

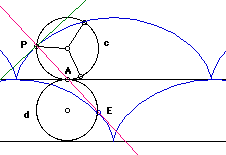
In the right figure, c is the rolling circle. P is the tracing point. A is the point of contact with line. PA is the normal at P. E is a reflection of P through A. The locus of E is the evolute of the cycloid.

Formula

• Parametric: {t - Sin[t], 1 - Cos[t]}

Properties

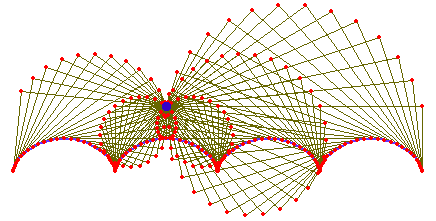
Caustic

The catacaustic of a cycloid with respect to parallel rays coming beneath its arc are two smaller cycloids. (Or, the diacaustic of the cycloid with rays coming from above.)

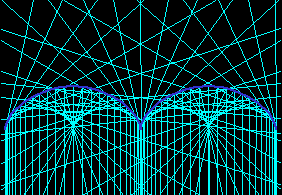
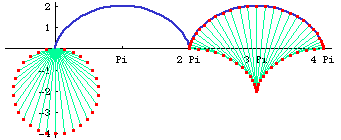
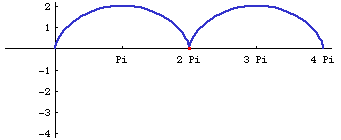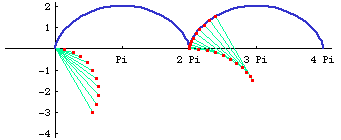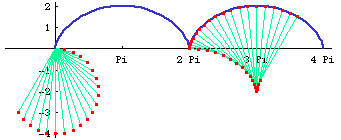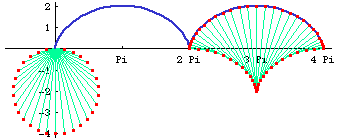
Evolute and Involute

The evolute of a cycloid is another cycloid. The first figure show succesive evolutes of a cycloid. The second connect points on the curve with their center of osculating circles.

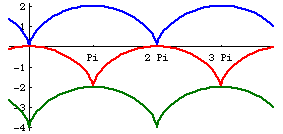
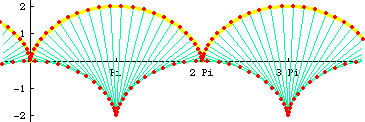
The involute of a cycloid is also a cycloid. Both evolute and involute properties are easily proved by a direct application of the formula and simplify the result.

Radial

The radial of a cycloid is a circle.

Related Web Sites

See: Websites on Plane Curves, Plane Curves Books .

Robert Yates: Curves and Their Properties .

The MacTutor History of Mathematics archive

Brombacher Aarnout, with GSP and QuickTime movies. http://jwilson.coe.uga.edu/EMT668/EMT668.Student.Folders/BrombacherAarnout/EMT669/cycloids/cycloids.html

Joseph Portney. A somewhat detailed exposition on the property of cycloid being the curve of fastest decent. (called brachistochrone) http://www.navworld.com/navcerebrations/millennium/millennium.htm