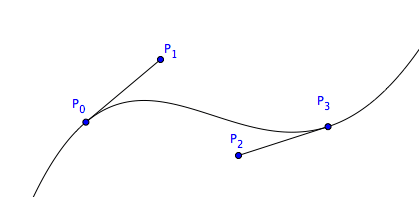
Bezier Curve
Description
“Bezier Curve” is a method of generating smooth curve in computer graphics. Note that it is a method of curve representation, and not a curve in the usual sense in math contexts.
The Bezier Curve method is named after the engineer Pierre Bézier .
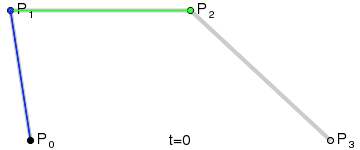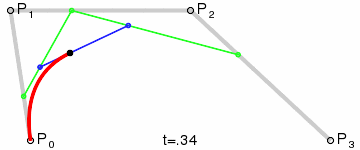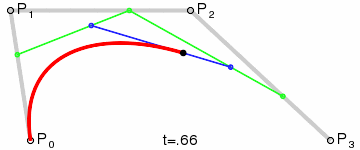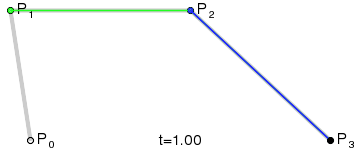
Given 4 points P0, P1, P2, P3, find a parametric formula in polynomial such that it passes P0 with tangent vector[P0,P1], and passes P2 with tangent vector[P3,P2].
Solution, written in complex number notation:
z[t]=(1-t)^3*P0 + 3*t(1-t)^2*P1 + 3*t^2(1-t)*P2 + t^3*P3
We verify that
z[0]==P0, z'[0]==3*(P1-P0) z[1]=P2, z'[1]==3*(P2-P3)