Nephroid
History
Studied by Huygens and Tschirnhausen about 1679 in connection with the theory of caustics. Jacques Bernoulli in 1692 showed that the nephroid is the catacaustic of a cardioid for a luminous cusp. Double generation was first discovered by Daniel Bernoulli in 1725. [Robert C Yates]
The name nephroid (“kidney-shaped”) was used for the two-cusped epicycloid by Proctor in 1878; a year later, Freeth used the same name for another curve (Freeth's Nephroid). [E.W.Lockwood]
Description
Nephroid is a special case of epi/hypocycloid. (See: Curve Family Index) Nephroid can be defined as the trace of a point fixed on a circle of radius 1/2 r that rolls outside a fixed circle with radius r. Also, it is the trace of a point fixed on a circle of radius 3/2 r that rolls inside a fixed circle of radius r. (by “inside”, it means the curvature of both circles at the contact point face the same direction) The latter is known as double generation.
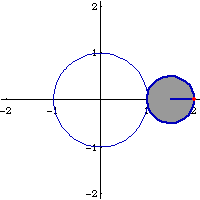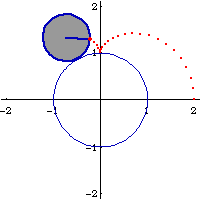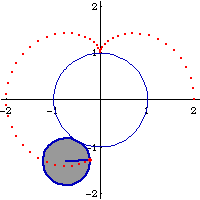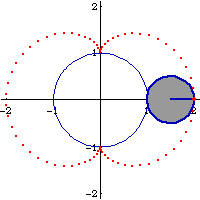
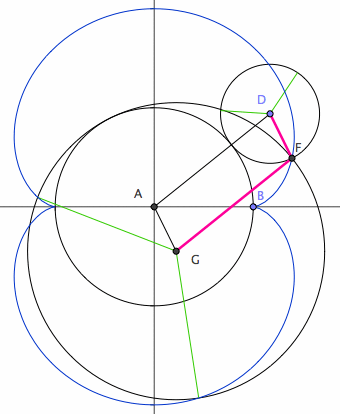
The two sizes of rolling circles that generate the nephroid can be synchronized by a linkage. (this means: the 2 roulette methods trace the curve with the same speed and have a geometric relation) Let A be the center of the fixed circle. Let D be the center of the smaller rolling circle. Let F be a fixed point on this circle (the tracing point). Let G be a point translated from A by the vector DF. G is the center of the large rolling circle, with the same tracing point at F. ADFG is a parallelogram with sides having constant lengths.
Formula
These formulas describe a nephroid with distance from cusp to cusp 4*a, where a is a scaling factor.
- Parametric: {3*Cos[t]-Cos[3*t],3*Sin[t]-Sin[3*t]}*a. 0 < t ≤ 2 Pi.
- Cartesian: (x^2+y^2-4*a^2)^3 == 108*a^4*y^2.
Not verified:
- s == 6*a*Sin[1/2*phi].
- s == 6*a*(1-Cos[1/2*psi]), 0 < psi < 2 Pi.
- Pedal: 4*r^2-3*p^2==16*a^2.
- Length: 24*a.
- Area: 12*Pi*a^2.
- Surface of revolution: 128/5*Pi*a^2.
Properties
Curve Construction
Nephroid's tangent, normal, center of curvature can be constructed.
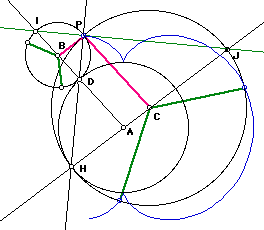
A is the center of the fixed circle with radius r. B is the center of the rolling circle with radius r/2. P is the tracing point. D is the point of contact. PDH are colinear. HACJ are colinear, where C is r/2 from A, and J is the reflection of H through C. C forms the center of the larger rolling circle with radius CH = 3/2 r. JPI is colinear and is the tangent at P. PD is the normal at P. Let Q (not shown) be the point formed by rotating P around B by 180 degrees. The intersection of AQ, PD forms the center of osculating circle at P. We call the line from cusp to cusp the diameter of the nephroid.
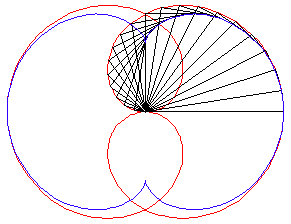
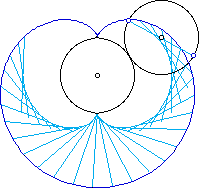
Catacaustic of a Circle or Cardioid
Nephroid is the catacaustic of a circle with parallel rays. (Left figure: half of nephroid is generated by rays coming from above.) Nephroid is the catacaustic of a cardioid with lightsource at the cusp.

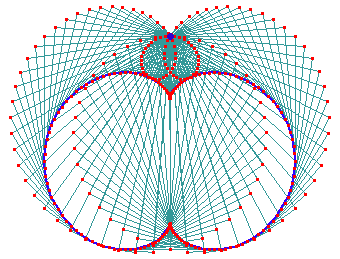
Envelope of Circles and Tangent Construction
Nephroid is the envelope of a set of circles with centers on a base circle B and tangent to a fixed diameter of B. (See left figure. Base circle is not shown) Nephroid is the envelope of a diameter of the circle that generates a cardioid as a epicycloid. (center figure) The normal of a nephroid is the line from the tracing point P on the rolling circle to the point of contact D.
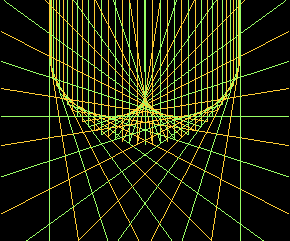
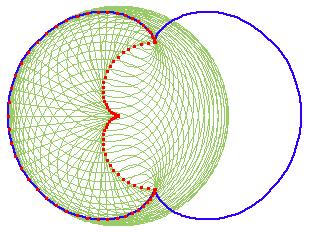
Evolute
Nephroid's evolute is equal to itself. (rotated Pi/2 radians and scaled by 1/2) (all epi/hypocycloids' evolute is equal to themselves) The left figure connects points on the curve to their centers of osculating circles. Only half are shown for clarity. The right figure uses envelope of normals to illustrate.

Reconcile Properties
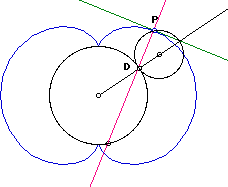
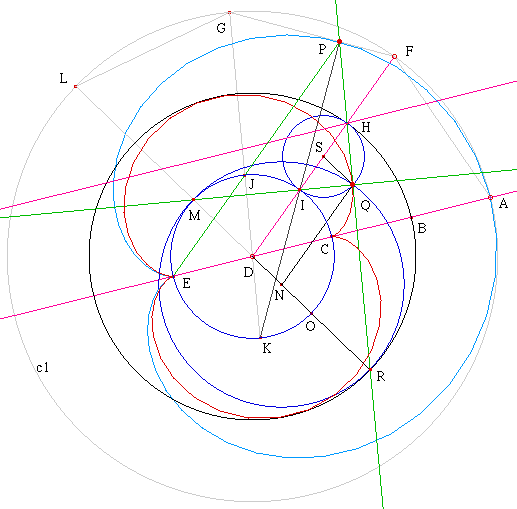
Here are all above mentioned properties in a single setting. We have a nephroid centered on D and diameter CE. Let A,B be points such that A,B,C,D,E are colinear and equally spaced. Construct three circles centred on D and passing A, B, C, and call them circle A, B, C. Let Q be any point on the nephroid. The tangent at Q intersect the circle B in two points H, R. Let F:=intersection[DH,circle A], I:=intersection[DH, circle C], S:=midpoint[H,I]. Let G be A reflected through DF (G:=reflect[A,DF]), and L:=reflect[F,DG], J:=intersection[DG,circle C], M:=intersection[DL,circle C], P:=intersection[QH,EJ], T:=reflected[Q,S] (T not shown).
- The reflection of HQ through DF is parallel to the diameter CE. This makes a nephroid being the catacaustic of a circle with parallel rays.
- Cardioid relation: P is a point on a cardioid with diameter AE. P is fixed on a circle centered on H and diameter HF, rolling on a fixed circle[D,DC]. The nephroid has half the area of the cardioid.
- Catacaustic of Cardioid: PI bisects angle QPE.
- Envelope of circle: circle[I,IQ] (not shown) is tangent to CE.
- QI is the normal at Q. QIM are colinear.
- Tangent circle: The midpoint of TD is the center of osculating circle at Q. (not shown)
- Other properties can be easily related.
Pedal, Radial, and Rose
The pedal of a nephroid with respect to its center is the a two-petalled rose r==Cos[1/2*θ]. The radial of a nephroid is the same rose. (The pedal and radial of epi/hypocycloids are roses. See each page for the general theorem.) In the following figure, the red curve is the rose.