Cissoid of Diocles

History

Diocles (~250 to ~100 BC) invented this curve to solve the doubling the cube problem. The name cissoid (ivy-shaped) came from the shape of the curve. Later the method used to generate this curve is generalized, and we call curves generated this way as cissoids .

From Thomas L Heath's Euclid's Elements translation (1925) (comments on definition 2, book one):

This curve is assumed to be the same as that by means of which, according to Eutocius, Diocles in his book On burning-glasses solved the problem of doubling the cube.

From Robert Yates:

As early as 1689, J. C. Sturm, in his Mathesis Enucleata, gave a mechanical device for the constructions of the cissoid of Diocles.

From E H Lockwood A book of Curves (1961):

The name cissoid ('Ivy-shaped') is mentioned by Geminus in the first century B.C., that is, about a century after the death of the inventor Diocles. In the commentaries on the work by Archimedes On the Sphere and the Cylinder, the curve is referred to as Diocles' contribution to the classic problem of doubling the cube. … Fermat and Roberval constructed the tangent (1634); Huygens and Wallis found the area (1658); while Newton gives it as a example, in his Arithmetica Universalis, of the ancients' attempts at solving cubic problems and again as a specimen in his Enumeratio Linearum Tertii Ordinis.

Description

Cissoid of Diocles is a special case of (general) cissoid. It is a cissoid of a circle and a line tangent to the circle with respect to a point on the circle opposite to the tangent point.

Step-by-step description:

1. Let there be a circle C and a line L tangent to this circle.
2. Let O be the point on the circle opposite to the tangent point.
3. Let P1 be a point on the circle C.
4. Let P2 be the intersection of line[O,P1] and L.
5. Let Q be a point on line[O,P1] such that distance[O,Q] == distance[P1,P2].
6. The locus of Q (as P1 moves on C) is the cissoid of Diocles.

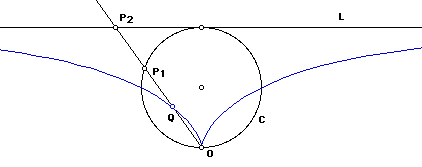
A important property to note is that Q and P1 are symmetric with respect to the midpoint of segment[O,P2]. Call this midpoint M. We can reflect every element in the construction around M, which will help us visually see other properties.

Formula derivation

• Let the given circle C be centered on {1/2,0} with radius 1/2, the given line L be x==1, and the given point O be the origin.
• Let P1 be a variable point on the circle, and Q the tracing point on line[O,P1].
• Let the point {1,0} be A.
• We want to describe distance[O,Q] in terms of angle[A,O,P1].
• This will give us a polar equation.
• From elementary geometry, triangle[A,O,P1] is a right triangle.
• By elementary trig, distance[O,P1]==Cos[θ].
• Similarly, triangle[O,A,P2] is a right triangle and distance[O,P2]==1/Cos[θ].
• Since distance[O,Q]==distance[O,P2]-distance[O,P1], we have distance[O,Q]==1/Cos[θ]-Cos[θ].
• Thus the polar equation is r==1/Cos[θ]-Cos[θ].
• Combine the fractions, and use identity 1==Sin[t]^2+Cos[t]^2, we arive at a alternative form r == Sin[θ] * Tan[θ].

Formula

In the following, the cusp is at the origin, and the asymptote is x==1. (the diameter of the circle is 1.)

• Parametric: {Sin[t]^2, Sin[t]^2*Tan[t]}, -Pi/2 < t < Pi/2.
• Parametric: {1,t}*(t^2/(1+t^2)), -Infinity < t < Infinity.
• Polar: r == 1/Cos[θ]-Cos[θ], -Pi/2 < t < Pi/2.
• Cartesian: y^2 * (1-x) == x^3

Properties

Doubling the Cube

Given a segment[C,B], we can construct a segment[C,M] such that distance[C,M]^3==2*distance[C,B]^3, with the help of cissoid of Diocles. This solves the famous doubling the cube problem.

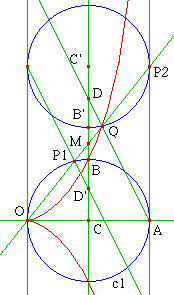
Step-by-step description:

1. Given two points C and B.
2. Construct a circle c1, centered on C and passing B.
3. Construct points O and A on the circle such that line[O,A] is perpendicular to line[C,B]
4. Construct a cissoid of Diocles using circle c1, tangent at A, and pole at O.
5. Construct point D such that B is the midpoint of segment[C,D].
6. Construct line[A,D]. Let the intersection of cissoid and line[A,D] be Q. (the intersection cannot be found with Greek Ruler and Compass. We assume it is a given.)
7. Let the intersection of line[C,D] and line[O,Q] be M.
8. length[C,M]^3==2*distance[C,D]^3.

This can be trivially proven with analytic geometry. is there a intuitive proof? (Extra figures in the figure are prepared for later comments.) proof by algebra

Diocles's construction

By some modern common accounts (Morris Kline, Thomas L. Heath), here's how Diocles constructed the curve in his book On Burning-glasses:

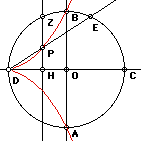
• Let AB and CD be perpendicular diameters of a circle.
• Let E be a point on arc[B,C], and Z be a point on arc[B,D], such that BE, BZ are equal.
• Draw ZH perpendicular to CD.
• Draw ED.
• Let P be intersection[ZH,ED].
• The cissoid is the locus of all points P determined by all positions of E on arc[B,C] and Z on arc[B,D] with arc[B,E]==arc[B,Z].
• (the portion of the curve that lies outside of the circle is a latter generalization).

• In the curve, we have CH/HZ==HZ/HD==HD/HP.
• Thus HZ and HD are two mean proportionals between CH and HP.

• Proof
• taking CH/HZ==HZ/HD, we have CH*HD==HZ^2.
• triangle[D,C,Z] is a right triangle since it's a triangle on a circle with one side being the diameter (elementary geometry).
• We know a angle[D,C,Z] and one side distance[D,C], thus by trigonometry of right angles, we can derive all lengths DZ, CZ, and HZ.
• Substituting the results of computation in CH*HD==HZ^2 results a identity.
• Similarly, we know length HP and find HZ/HD==HD/HP to be a identity.

Newton's Carpenter's Square and Tangent

Newton showed that cissoid of Diocles can be generated by sliding a right triangle. This method also easily proves the tangent construction.

Step-by-step description:

1. Let there be two distinct fixed points B and O, both on a given line j. (distance[B,O] will be the radius of the cissoid of Diocle we are about to construct.)
2. Let there be a line k passing O and perpendicular to j.
3. Let there be a circle centered on a arbitrary point C on k, with radius OB.
4. There are two tangents of this circle passing B, let the tangent points be E and F.
5. Let I be the midpoint between E and the center of the circle. Similarly, let J be the midpoint between F and the center of the circle.
6. The locus of I and J (as C moves on k) is the cissoid of Diocles and a line. Also, the locus of E and F is the right strophoid.

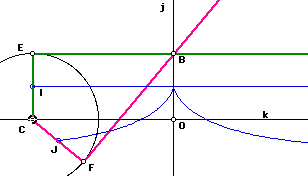
Tangent construction: Think of triangle[C,F,B] as a rigid moving body. The point C moves in the direction of vector[O,C], and point B moves in the direction of vector[B,F]. The intersection H (not shown) of normals of line[O,C] and line[B,F] is its center of rotation. Since the tracing point J is a point on the triangle, thus HJ is normal to the curve.

Pedal and Cardioid

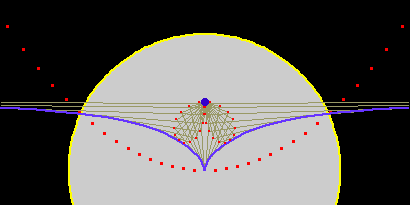
The pedal of a cissoid of Diocles with respect to a point P is the cardioid. If the cissoid's asymptote is the line y = 1 and its cusp is at the origin, then P is at {0,4}. It follows by definition, the negative pedal of a cardioid with respect to a point opposite its cusp is the cissoid of Diocles.

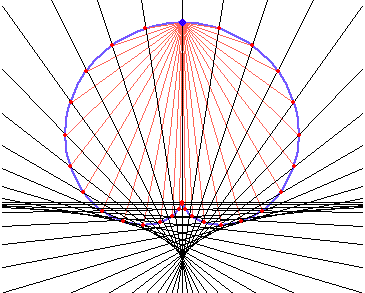
Negative Pedal and Parabola

The pedal of a parabola with respect to its vertex is the cissoid of Diocles. (and then by definition, the negative pedal of a cissoid of Diocles with respect to its cusp is a parabola.)

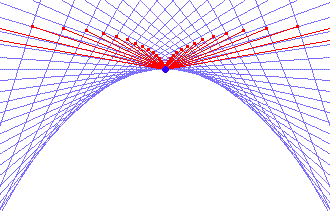
Inversion and Parabola

The inversion of a cissoid of Diocles at cusp is a parabola .

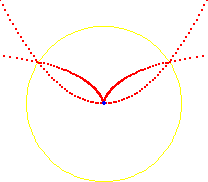
Misc

as Roulette of a Parabola

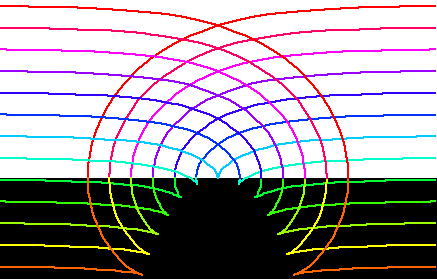
Let there be a fixed parabola. Let there be a equal parabola that rolls on the given parabola in such way that the two parabolas are symmetric to the line of tangency. The vertex of the rolling parabola traces a cissoid of Diocles.

prove that cissoid of Diocles is a roulette of a parabola on a parabola.

Gallery

Related Web Sites

• Websites on Plane Curves
• Plane Curves Books
• Curves and Their Properties: Cissoid, p026
• https://mathshistory.st-andrews.ac.uk/Curves/Cissoid/