Trisectrix

Description
Trisectrix is a general name for curves that can be used to trisect a angle. The name trisectrix is often reserved for a special case of limacon of Pascal, which we discuss here. Other famous trisectrix include trisectrix of Maclaurin and conchoid of Nicomedes.
Trisectrix can be generated as a conchoid or epitrochoid. (See: limacon of Pascal for definition).
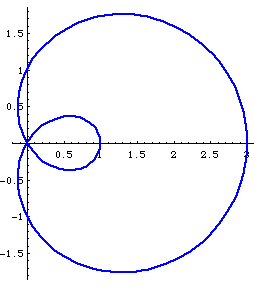
Formula
- Polar: r == (1+2 * Cos[t]) , 0 ≤ t < 2 Pi.
- Cartesian: (-2 x + x^2 + y^2)^2 == x^2 + y^2
Properties
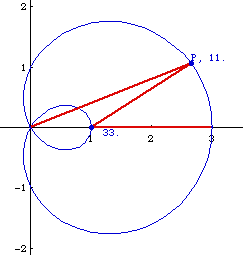
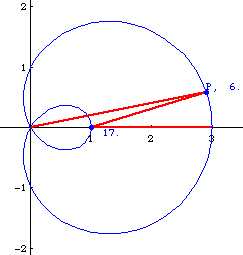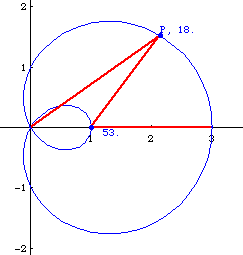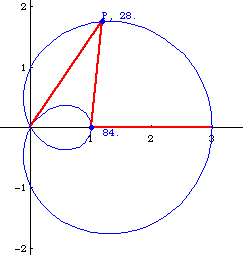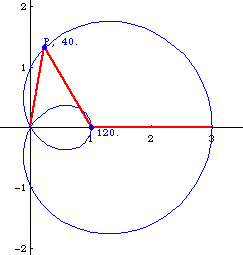
Trisecting a Angle
Let P be any point on the outer loop of the curve. The angle formed by P, {1,0}, {3,0} is three times larger than the angle {0,0}, P, {1,0}.
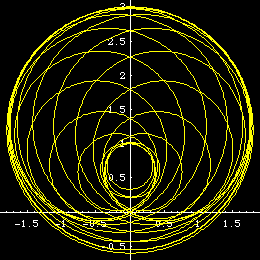
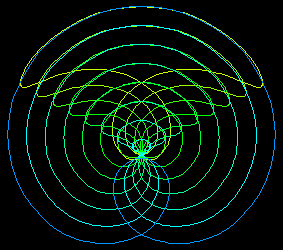
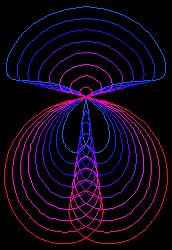
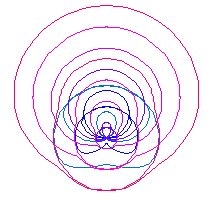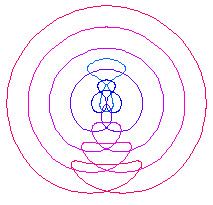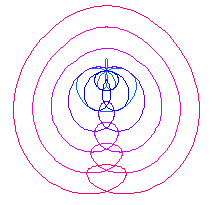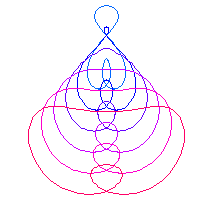
Graphic Gallery
Parallels of trisectrix.