Quadratrix Of Hippias
Mathematica Notebook for This Page .
History
Quadratrix of Hippias is the first named curve other than circle and line. It is conceived by Hippias of Ellis (~460 BC) to trisect the angle thus sometimes called trisectrix of Hippias. The curve is better known as quadratrix because it is later used to square the circle .
Description
Step by step description:
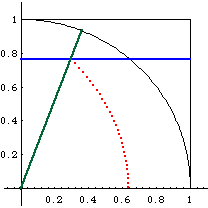
- Let there be a unit square in the first quardrant with lower-left coner at the origin.
- Let there be a line parallel to the x-axis and gradually moving up at a constant speed from the bottom side of the square until it reaches the upper side of the square.
- Let there be a angle in standard position. The angle increase at a constant speed from 0 to Pi/2. Both the angle and line movement start and finish simultaneously.
- The intersections of the line and the angle is quadratrix of Hippias.
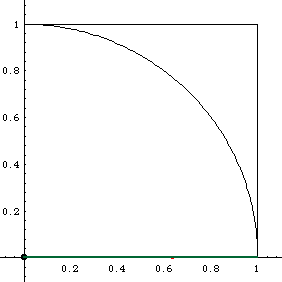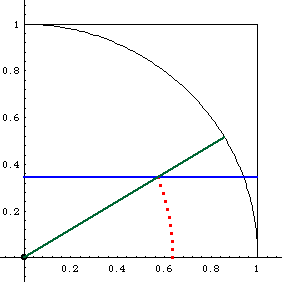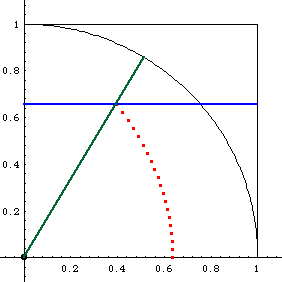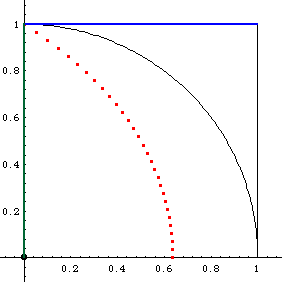
Given the definition, it is easy to derive the parametric equation. Let the parameter t be the angle, 0 < t < Pi/2 and the square having side length Pi/2. So immediately, y == t. Since we know the angle and one side of the triangle y at any time t, using the identity Cot[t] = x/y to get the formulas.
Formula
- Polar: r == θ/Sin[θ]
- Cartesian: x == y * Cot[y]
Properties
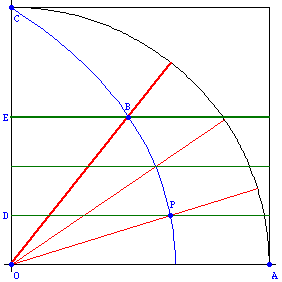
Trisecting a Angle
The curve can be used to trisect any acute angle. To trisect angel AOB, one first find distance OE, take one third of distance OE to get OD (trisection of a segment can be done with ruler and compass). Let the intersection of the curve and the horizontal line at D be P, then the angle AOP is one third of angle AOB. This follows because by the definition of the curve, distance[O,E]/distance[O,C] == angle[A,O,B]/(Pi/2). If distance[O,C] == Pi/2, then distance[O,E] == angle[A,O,B].
