Semicubic Parabola
Mathematica Notebook for This Page .
History
From Robert Yates:
a*y^2==x^3 was the first algebraic curve rectified (Neil 1659). Leibnitz in 1687 proposed the problem of finding the curve down which a particle may descend under the force of gravity, falling equal vertical distances in equal time intervals with initial velocity different from zero. Huygens announced the solution as a semi-cubic parabola with a vertical cusp tangent.
Description
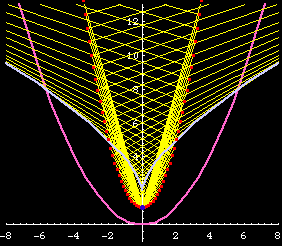
Semicubic parabola is defined as the evolute of parabola. In the figure, normals (light blue) of a parabola (purple) are drawn. The envelope of these lines is the semicubic parabola.
Formula
- Parametric: Parametric: {t^3, t^2}.
- Polar: r == Tan[t]^2 * Sec[t]
- Cartesian: x^2 == y^3
{t^3, t^2} is the evolute of the parabola {(-4 t)/9, -8/27 + t^2/3}.
Properties
Unstretchable
The parabola {(-4 t)/9, -8/27 +t^2/3} is the parabola {t,1/4 t^2} scaled by a factor of 4/27 and translated by {0, -8/27}.
Semicubic parabola inherets the property from parabola that when streched horizontally or vertically, the curve remain unchanged. That is, the curve {a t^3, b t^2} is equivalent to {t^3, t^2}*(b^3/a^2). This is why sometimes you'll see different equations like {2 t^3, 3 t^2} for it.
The pedal of a semicubic parabola with respect to the focus of a parabola the semicubic parabola is derived from is another parabola. In the figure below, the pink curve is the original parabola, blue dot is its focus. The evolute of it is the semicubic parabola (bluish-white). Its pedal is rendered as red dots, which is another parabola.
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .