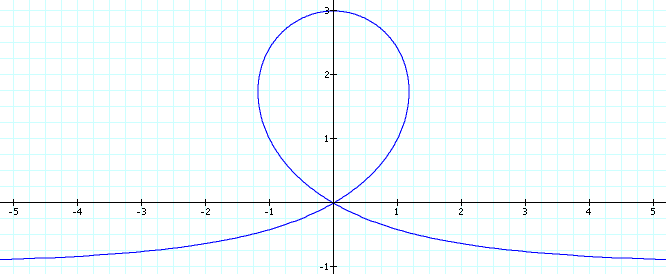
Trisectrix of Maclaurin
History
This is a curve Colin Maclaurin (1698 to 1746) used to trisect a angle.
Description
Formula
The following formula has asymtote at x=1 and loop point at origin:
Polar: r==Sec[t] - 4 Cos[t], -Pi/2 < t < Pi/2.
Parametric: (1-4 Cos[t]^2)*{1, Tan[t]}, -Pi/2 < t < Pi/2.
Parametric: {(-3 + t^2)/(1 + t^2), (t*(-3 + t^2))/(1 + t^2)}, -Infinity < t < Infinity.
Cartesian: y^2 (1-x) == x^2 (x + 3)
Polar: r==Sec[t/3], -3/2 Pi < t < 3/2 Pi. (vertex at {1,0}, double point at {-2,0})
Properties
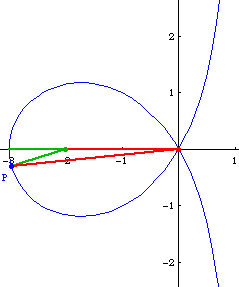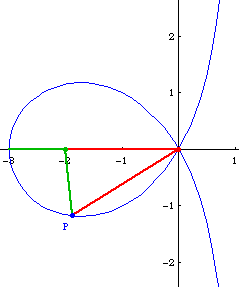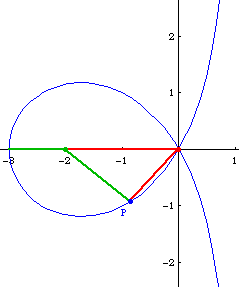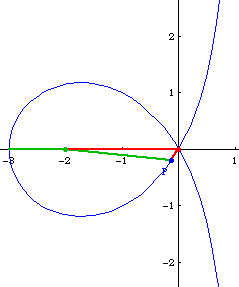
Relation to Parabola
It is the pedal of parabola with repect to its focus reflect by the directrix.
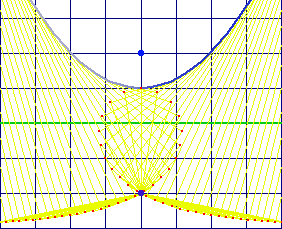
Trisecting a Angle
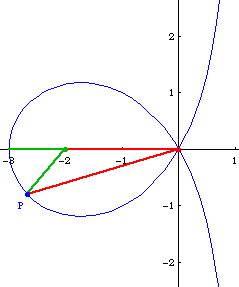
Suppose we have a trisectrix with node at the origin and vertex at point {-3,0}, and let P be any point on the loop of the curve. angle[{-3,0},{-2,0},P] == 3*angle[{-2,0},{0,0},P].