Witch of Agnesi
Mathematica Notebook for This Page .
History
Studied by Maria Gaetana Agnesi (1718 to 1799) in 1748. Also studied by Fermat (1666), and Guido Grandi (1703). The name of this curve has a colorful history. Versaria is the name given by Grandi, meaning “turning in every direction”. In the course of time the word versariatook on another meaning. The Latin words adversaria, and by aphaeresis, versaria, signify a female that is contrary to God. Thus gradually the curve versaria is understood in English as the Witch.
Description
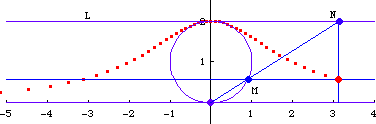
Witch of Agnesi (Versiera) is defined as follows.
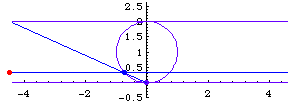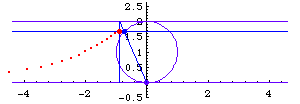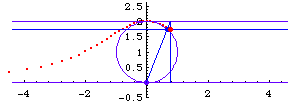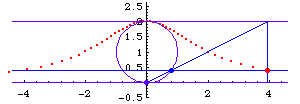
Step by step description:
- Let there be a circle of radius a with center at {0,a}.
- Let there be a horizontal line L passing through {0,2 a}.
- Draw a line passing the Origin and any point M on the circle. Let the intersection of this secant and line L be N.
- Witch of Agnesi is the locus of intersections of a horizontal line passing through M and a vertical line passing through N.
Formula
Let the construction circle be centered at {0,1} with radius 1, then:
- Parametric: {2*t, 2/(1+t^2)}, 0 < t < ∞.
- Parametric: 2 {Tan[t], Cos[t]^2}, -π/2 < t < π/2.
- Cartesian: y*(x^2+4)==8
The parametric equation {2*t, 2/(1+t^2)} is derived easily by starting with a equation of circle x^2+(y-1)^2==1 and a line y==t*x and solve the equation of circle and lines, and simplify the result by the replacement t→1/t. (or, start with y==1/t*x instead). Elimating t and we find the Cartesian equation.
Properties
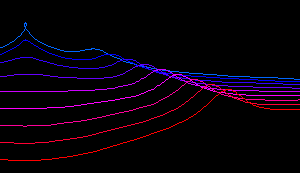
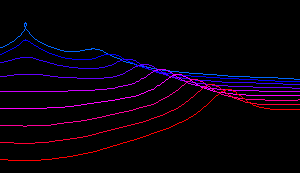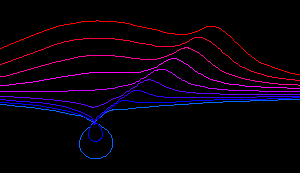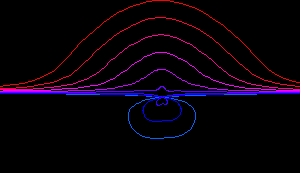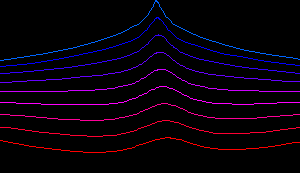
Graphics Gallery
Normals, and Evolute of witch of Agnesi.
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .