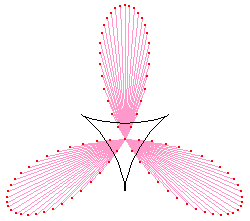
Deltoid
Mathematica Notebook for This Page .
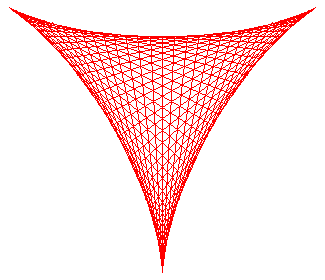
History
Conceived by Euler in 1745 in connection with a study of caustics curves.
Description
Deltoid (aka tricuspid) is a special case of hypocycloid. (See: Curve Family Index)
Deltoid can be defined as the trace of a point on a circle, rolling inside another circle 3 or 3/2 times as large in radius. The latter is called double generation.
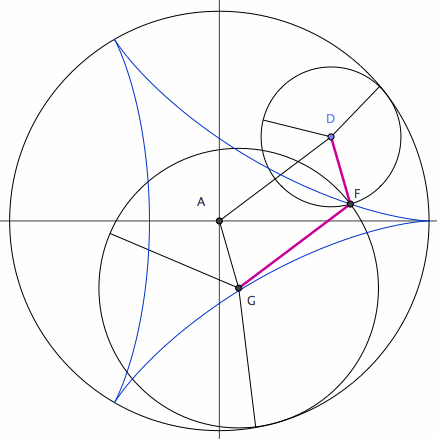
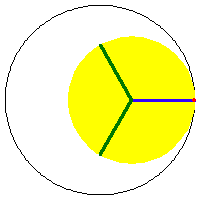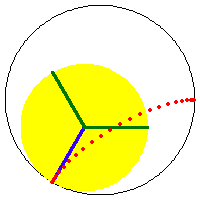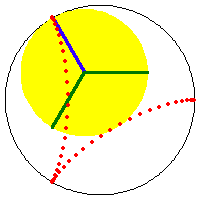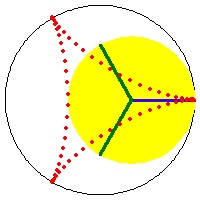
The two sizes of rolling circles that generate the deltoid can be synchronized by a linkage. (this means: the 2 roulette methods trace the curve with the same speed and has a geometric relation) Let A be the center of the fixed circle. Let D be the center of the smaller rolling circle. Let F be a fixed point on this circle (the tracing point). Let G be a point translated from A by the vector DF. G is the center of the large rolling circle, with the same tracing point at F. ADFG is a parallelogram with sides having constant lengths.
Formula
- Parametric: {(2 Cos[t]) + Cos[2 t], (2 Sin[t]) - Sin[2 t]}, 0 < t ≤ 2 π.
- Cartesian: (x^2+y^2)^2-8 x (x^2 - 3 y^2) + 18 (x^2 + y^2) - 27 == 0
Properties
Curve Construction
The deltoid is rich in properties. Its locus, tangent, and center of osculating circle can be constructed. If given a segment of unit 1 with 1/3 marked, then the curve can be constructed with ruler and compass.
Let there be a circle c centered on O passing B. We will construct the curve centered on O with one cusp at B. Let O be the origin, and B be the point {1,0}. Let J be a variable point on c. Construct a point E on c such that angle[B,O,E] == - 2*angle[B,O,J]. Construct a circle d, centered on O with radius 1/3 of circle c. The line OE intersect d at 2 places. Let A be the intersection of d and segment OE. Let G be the (other) intersection of d and line OE. Let P be a point on line JE such that GP and JE are perpendicular. Now, the point P is the locus of deltoid as J varies. GP is its tangent. JE is its normal.
To construct the osculating circle: Let k be a circle with radius 2/3 of c. Let H be the intersection of k and OJ. Let Q be the mirror of P thru H. The intersection of OQ and EJ is the center of osculating circle at P.
Further, H is the center of the smaller rolling circle with tracing point at P, and A is the center of the larger rolling circle with tracing point at P. Points OHPA is a parallelogram with constant sides.
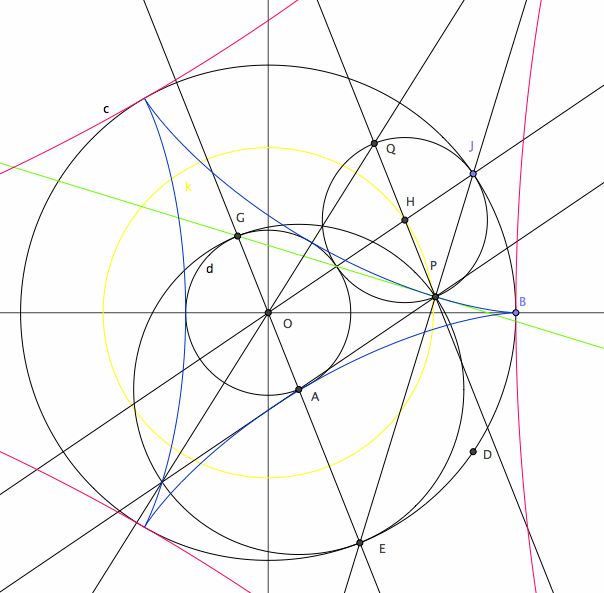
Tangent
Let A be the center of the curve. Let B be one cusp, P be any point on the curve. Let E, H be the intersections of the curve and the tangent at P. The segment EH has constant length distance[E,H]== 4/3*distance[A,B]. The locus of midpoint D of tangent segment EH is the inscribed circle. The normals at E,P,H are concurrent, and its locus is the circumscribed circle. Let J be the intersection of another tangent cutting EH at right angle. The locus of J (deltoid's orthoptic) is the inscribed circle.
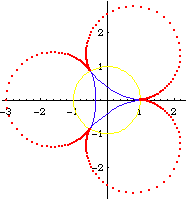
Deltoid and Astroid
Astroid is the caustic of deltoid with parallel rays in any direction.
prove the caustic relation between deltoid and astroid.
Evolute
put proof that the deltoid evolute is a deltoid.
The evolute of deltoid is another deltoid. (all epi/hypocycloids' evolute are equal to themselves) In the left figure, the evolute is formed by the envelope of its normals. The right figure show osculating circles and their centers.
Inversion
A inversion of deltoid with respect to its center.
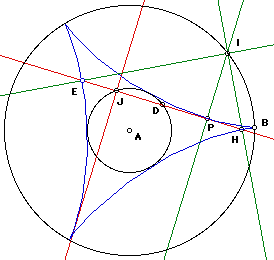
Simson Lines
prove that deltoid is envelope of Simson lines
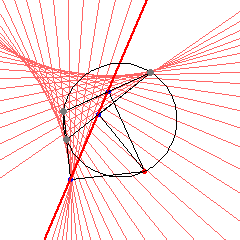
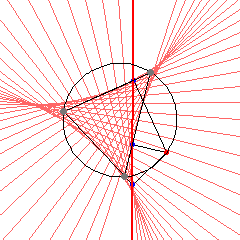
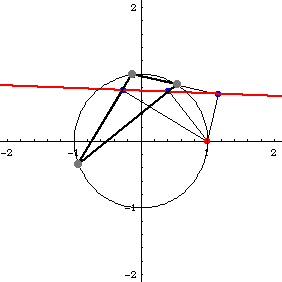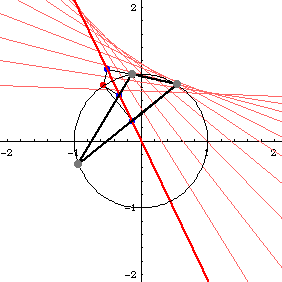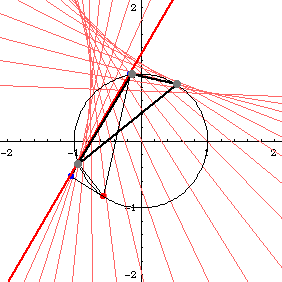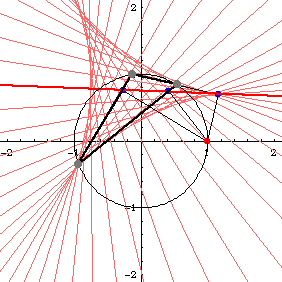
Deltoid is the envelope of Simson lines of any triangle. (Robert Simson, 1687 to 1768). Step by step description:
- Let there be a triangle inscribed in a circle.
- Pick any point P on the circle.
- Mark a point Q1 on any side of the triangle such that line[P,Q1] is perpendicular to it. Extend the side if necessary.
- Similarly, find points Q2 and Q3 with respect to P for other sides.
- The points Q1, Q2, and Q3 are colinear. The line passing through them is called Simson line of the triangle with respect to P.
- Find Simson lines for other points P on the circle. The envelope of Simson lines is the deltoid. Amazingly, this is true for any triangle.
Pedal, Radial, and Rose
prove deltoid's radial, pedal, rose curves
The pedal of deltoid with respect to a cusp, vertex, or center is a folium with one, two, or three loops respectively. The last one is called trifolium, which is a 3-petaled rose. Deltoid's radial is a trifolium too. (all epi/hypocycloid's pedal and radial are equal, and they are roses.) Conjectures: (1) 60 degree isoptic of deltoid is a inscribed trifolium. visual proof (2) The derivative of deltoid's parametric equation is also a trifolium.
Deltoid as Roulette Constructing Tangent Circle
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .