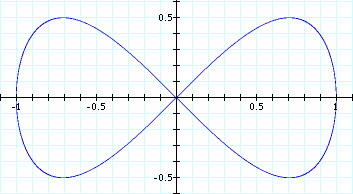
Lemniscate of Gerono
History
Studied by Camille-Christophe Gerono (1799 to 1891).
Description
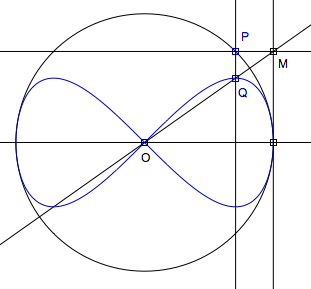
Lemniscate of Gerono is also known as the figure eight curve. It can be constructed as follows: Let there be a circle of radius 1 centered on the Origin. Let P be a point on the circle. Let M be the intersection of x==1 and a horizontal line passing P. Let Q be the intersection of line OM and a vertical line passing P. The trace of Q as P moves on the circle is the Figure Eight curve.
Formula
- Parametric: {1,Sin[t]}*Cos[t], Period: 2 π.
- Cartesian: x^4 == x^2 - y^2
The parametric formula is directly derived. Starting with P:={Cos[t],Sin[t]}. The vertical line passing P would be x==Cos[t]. The point M would be {1,Sin[t]}. Solving for the insersection of line OM and x==Cos[t] results the formula.
For the Cartesian formula, eliminate the trig terms in x==Cos[t], y==Cos[t]*Sin[t] by squaring both side and add the two equations and use the identity Cos[t]^2+Sin[t]^2==1.
Properties
Second Construction
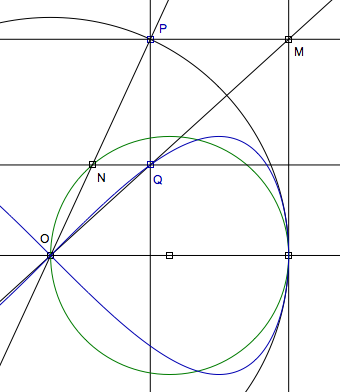
Let there be a circle centered on {1/2,0} of radius 1/2. Let N be the intersection of the circle and line OP. The intersection Q of vertical line thru P and horizontal line thru N traces the curve.
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
The Construction property is from http://www.mathcurve.com/courbes2d/gerono/gerono.shtml by Robert Ferreol, Jacques Mandonnet.